常微分方程和差分方程

更新于 分类于 阅读次数： 本文字数： 10k 阅读时长 ≈ 17 分钟
点击阅读全文

第四章-常微分方程和差分方程

习题1

\[ 2x_{n+2}-x_{n+1}-2x_{n}=0 \]

并且初值为\(x_0=-2;x1=0;\)

解法一：

其对应的特征方程为：

\[ 2\lambda^2-\lambda-2=0 \]

求解特征值可以通过一元二次方程的公式求解，也可以通过scipy直接求解。

求解出的特征值有两个，不是重根，分别为\(\lambda_1,\lambda_2\)，则其通解为 \[ x_n=C_1\lambda_1^n+C_2\lambda_2^n \]

其中C1和C2常量由初始条件求出。

解法二：

通过迭代法求出$ x_n $对应的数值解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import math
print("----通过math计算特征方程的根----")

a = 2
b = -1
c = -2
d=b**2-4*a*c
if (d<0):
    print("无解")
else:
    e = math.sqrt(d)
    x1=((-b+e)/(2*a))#调用math模块中sqrt开平方函数
    x2=((-b-e)/(2*a))
    print("landa1=",x1,"\t","landa2=",x2)

import sympy as sp
#solve函数可以直接求解

print("----通过sympy计算特征方程的根和最终结果----")
sp.var('t, c1, c2')
t0 = sp.solve(2*t**2-t-2)  #求解特征方程
eq1 = c1 + c2 + 2
eq2 = c1 * t0[0] + c2 *t0[1]
s = sp.solve([eq1, eq2])
print('landa1=',t0[0],'\t','landa2=',t0[1])
print('c1=', s[c1]); print('c2=', s[c2])

for i in range(2,10):
    print("x[",i,"]=",(s[c1]*pow(t0[0],i)+s[c2]*pow(t0[1],i)).evalf())
print('----通过迭代计算x(n)的数值解-----')
prev = -2;x = 0
for i in range(1,10):
    temp = x
    x = (x + 2*prev)/2
    print("x[",i+1,"]=",x)
    prev = temp


结果为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
----通过math计算特征方程的根----
landa1= 1.2807764064044151    landa2= -0.7807764064044151
----通过sympy计算特征方程的根和最终结果----
landa1= 1/4 - sqrt(17)/4    landa2= 1/4 + sqrt(17)/4
c1= -1 - sqrt(17)/17
c2= -1 + sqrt(17)/17
x[ 2 ]= -2.00000000000000
x[ 3 ]= -1.00000000000000
x[ 4 ]= -2.50000000000000
x[ 5 ]= -2.25000000000000
x[ 6 ]= -3.62500000000000
x[ 7 ]= -4.06250000000000
x[ 8 ]= -5.65625000000000
x[ 9 ]= -6.89062500000000
----通过迭代计算x(n)的数值解-----
x[ 2 ]= -2.0
x[ 3 ]= -1.0
x[ 4 ]= -2.5
x[ 5 ]= -2.25
x[ 6 ]= -3.625
x[ 7 ]= -4.0625
x[ 8 ]= -5.65625
x[ 9 ]= -6.890625
x[ 10 ]= -9.1015625

最终其结果为

\[ x_n=(-1-\frac{\sqrt17}{17})*(\frac{1-\sqrt17}{4})^n+(-1+\frac{\sqrt17}{17})*(\frac{1+\sqrt17}{4})^n \]

以上结果可以发现特征方程的解法和迭代解法的完全一致。

习题2

令\(x(t)=[x_1(t),x_2(t)]^T\)其中，\(x_1(t)=x,x_2(t)=y\)；则题目描述可以变成

\[ \frac{dx}{dt}=Ax,x(0)=[1,0]^T,A=\begin{bmatrix} %中括号 1&-2\\ 1&2 \end{bmatrix} \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import sympy as sp
from scipy.integrate import odeint
import numpy as np
import pylab as plt

#-------------求解析解----------------
sp.var('t')
sp.var('x1:3', cls=sp.Function) #定义2个符号函数
x = sp.Matrix([x1(t), x2(t)])  #列向量
A = sp.Matrix([[1,-2],[1,2]])
eq = x.diff(t)-A@x
s = sp.dsolve(eq, ics={x1(0):1, x2(0):0})
print("解析解为:",s);
sx = sp.lambdify(t,s[0].args[1],'numpy')  #符号函数转匿名函数
sy = sp.lambdify(t,s[1].args[1],'numpy')  #符号函数转匿名函数
xx = np.linspace(0,1,50)
plt.rc('font', family='SimHei')
plt.rc('axes', unicode_minus=False)
plt.rc('font', size=16)
plt.plot(sx(xx), sy(xx));
plt.xlabel('$x$')
plt.ylabel('$y$',rotation=0);


#-------------求数值解--------------
dx = lambda x, t: [x[0]-2*x[1],x[0]+2*x[1]]
t = np.linspace(0, 1, 50)
s = odeint(dx, [1,0], t)
plt.plot(s[:,0], s[:,1]);
plt.xlabel('$x$')
plt.ylabel('$y$',rotation=0);

print("=============具体结果为==================")
k = 0;
for i in np.linspace(0,1,50):
    print("t=",i,"时\n解析解求得:x(t)=",sx(i),"y(t)=",sy(i),"\n数值解求得:x(t)=",s[:,0][k],"y(t)=",s[:,1][k])
    k=k+1

plt.legend(['解析解','数值解'])
plt.show()


结果为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
D:\anaconda\envs\pytorch\python.exe "D:/pythonMath/Deffrential Equations/homework2.py"
解析解为: [Eq(x1(t), -sqrt(7)*exp(3*t/2)*sin(sqrt(7)*t/2)/7 + exp(3*t/2)*cos(sqrt(7)*t/2)), Eq(x2(t), 2*sqrt(7)*exp(3*t/2)*sin(sqrt(7)*t/2)/7)]
=============具体结果为==================
t= 0.0 时
解析解求得:x(t)= 1.0 y(t)= 0.0 
数值解求得:x(t)= 1.0 y(t)= 0.0
t= 0.02040816326530612 时
解析解求得:x(t)= 1.020189876647608 y(t)= 0.021040007527822792 
数值解求得:x(t)= 1.0201898879194644 y(t)= 0.021039997406066154
t= 0.04081632653061224 时
解析解求得:x(t)= 1.0399020205807203 y(t)= 0.043372287285719395 
数值解求得:x(t)= 1.0399020271650798 y(t)= 0.043372277714182235
t= 0.061224489795918366 时
解析解求得:x(t)= 1.0590724075998625 y(t)= 0.0670400680081496 
数值解求得:x(t)= 1.0590724185491094 y(t)= 0.0670400571843811
t= 0.08163265306122448 时
解析解求得:x(t)= 1.0776339017990748 y(t)= 0.09208701367564913 
数值解求得:x(t)= 1.0776339148814231 y(t)= 0.09208700197578465
t= 0.1020408163265306 时
解析解求得:x(t)= 1.0955161744257782 y(t)= 0.11855717598964706 
数值解求得:x(t)= 1.0955161877240351 y(t)= 0.11855716371338518
t= 0.12244897959183673 时
解析解求得:x(t)= 1.1126456231022948 y(t)= 0.14649494318063638 
数值解求得:x(t)= 1.112645634783687 y(t)= 0.14649492887241075
t= 0.14285714285714285 时
解析解求得:x(t)= 1.1289452915706144 y(t)= 0.1759449850061317 
数值解求得:x(t)= 1.1289452961242472 y(t)= 0.17594496400477785
t= 0.16326530612244897 时
解析解求得:x(t)= 1.1443347901312997 y(t)= 0.20695219379232827 
数值解求得:x(t)= 1.1443347993093749 y(t)= 0.20695217366966792
t= 0.18367346938775508 时
解析解求得:x(t)= 1.158730216957037 y(t)= 0.23956162137094936 
数值解求得:x(t)= 1.1587302335745913 y(t)= 0.23956160356463208
t= 0.2040816326530612 时
解析解求得:x(t)= 1.1720440804712116 y(t)= 0.27381841176044386 
数值解求得:x(t)= 1.1720440993327175 y(t)= 0.2738183930701502
t= 0.22448979591836732 时
解析解求得:x(t)= 1.184185222992092 y(t)= 0.3097677294384818 
数值解求得:x(t)= 1.1841852438829685 y(t)= 0.3097677096764967
t= 0.24489795918367346 时
解析解求得:x(t)= 1.1950587458536985 y(t)= 0.34745468305060684 
数值解求得:x(t)= 1.1950587687745 y(t)= 0.34745466091234584
t= 0.26530612244897955 时
解析解求得:x(t)= 1.204565936225206 y(t)= 0.3869242443979466 
数值解求得:x(t)= 1.2045659608485249 y(t)= 0.38692422094306006
t= 0.2857142857142857 时
解析解求得:x(t)= 1.2126041958618434 y(t)= 0.4282211625450773 
数值解求得:x(t)= 1.2126042225958342 y(t)= 0.42822113693988506
t= 0.3061224489795918 时
解析解求得:x(t)= 1.219066972031623 y(t)= 0.4713898728874819 
数值解求得:x(t)= 1.2190670009195195 y(t)= 0.4713898455557759
t= 0.32653061224489793 时
解析解求得:x(t)= 1.2238436908739307 y(t)= 0.5164744010165694 
数值解求得:x(t)= 1.223843722308065 y(t)= 0.5164743714132232
t= 0.3469387755102041 时
解析解求得:x(t)= 1.2268196934579962 y(t)= 0.5635182612189238 
数值解求得:x(t)= 1.2268197322675731 y(t)= 0.5635182204027751
t= 0.36734693877551017 时
解析解求得:x(t)= 1.227876174821546 y(t)= 0.6125643494453575 
数值解求得:x(t)= 1.227876226781901 y(t)= 0.6125642872253357
t= 0.3877551020408163 时
解析解求得:x(t)= 1.2268901262825176 y(t)= 0.6636548305844675 
数值解求得:x(t)= 1.2268901860909702 y(t)= 0.6636547583015104
t= 0.4081632653061224 时
解析解求得:x(t)= 1.223734281329584 y(t)= 0.716831019874726 
数值解求得:x(t)= 1.2237343409840549 y(t)= 0.7168309556017836
t= 0.42857142857142855 时
解析解求得:x(t)= 1.2182770654103952 y(t)= 0.7721332582887461 
数值解求得:x(t)= 1.218277123099709 y(t)= 0.7721332067917788
t= 0.44897959183673464 时
解析解求得:x(t)= 1.2103825499498861 y(t)= 0.8296007817231976 
数值解求得:x(t)= 1.210382610633588 y(t)= 0.8296007294438116
t= 0.4693877551020408 时
解析解求得:x(t)= 1.1999104109447043 y(t)= 0.8892715838279832 
数值解求得:x(t)= 1.1999104771822011 y(t)= 0.8892715275180807
t= 0.4897959183673469 时
解析解求得:x(t)= 1.1867158924938193 y(t)= 0.9511822723087026 
数值解求得:x(t)= 1.1867159642423326 y(t)= 0.9511822134138961
t= 0.5102040816326531 时
解析解求得:x(t)= 1.1706497756396121 y(t)= 1.0153679185371705 
数值解求得:x(t)= 1.170649853490215 y(t)= 1.0153678586747292
t= 0.5306122448979591 时
解析解求得:x(t)= 1.1515583529082627 y(t)= 1.0818619003058079 
数值解求得:x(t)= 1.1515584373707495 y(t)= 1.0818618396133117
t= 0.5510204081632653 时
解析解求得:x(t)= 1.1292834089530053 y(t)= 1.150695737563145 
数值解求得:x(t)= 1.129283497834692 y(t)= 1.1506956759804483
t= 0.5714285714285714 时
解析解求得:x(t)= 1.103662207718833 y(t)= 1.2218989209694522 
数值解求得:x(t)= 1.1036623018061529 y(t)= 1.2218988580689951
t= 0.5918367346938775 时
解析解求得:x(t)= 1.0745274865624315 y(t)= 1.2954987331136845 
数值解求得:x(t)= 1.0745275858196601 y(t)= 1.295498669179269
t= 0.6122448979591836 时
解析解求得:x(t)= 1.0417074577765977 y(t)= 1.3715200622355053 
数值解求得:x(t)= 1.0417075636067084 y(t)= 1.3715199970490806
t= 0.6326530612244897 时
解析解求得:x(t)= 1.0050258179840106 y(t)= 1.4499852082991638 
数值解求得:x(t)= 1.005025931367244 y(t)= 1.4499851416835472
t= 0.6530612244897959 时
解析解求得:x(t)= 0.9643017658810773 y(t)= 1.5309136812694661 
数值解求得:x(t)= 0.9643018849986369 y(t)= 1.530913614053574
t= 0.673469387755102 时
解析解求得:x(t)= 0.9193500288285735 y(t)= 1.6143219914440199 
数值解求得:x(t)= 0.9193501552672215 y(t)= 1.614321923290281
t= 0.6938775510204082 时
解析解求得:x(t)= 0.8699808988019734 y(t)= 1.7002234317003653 
数值解求得:x(t)= 0.8699810316861855 y(t)= 1.700223363015467
t= 0.7142857142857142 时
解析解求得:x(t)= 0.8160002782306479 y(t)= 1.7886278515215799 
数值解求得:x(t)= 0.816000418452806 y(t)= 1.7886277822226788
t= 0.7346938775510203 时
解析解求得:x(t)= 0.7572097362715636 y(t)= 1.8795414226694434 
数值解求得:x(t)= 0.7572098846938927 y(t)= 1.8795413527037244
t= 0.7551020408163265 时
解析解求得:x(t)= 0.6934065760796148 y(t)= 1.972966396380324 
数值解求得:x(t)= 0.6934067316386655 y(t)= 1.972966326317898
t= 0.7755102040816326 时
解析解求得:x(t)= 0.6243839136533351 y(t)= 2.0689008519656586 
数值解求得:x(t)= 0.6243840793830152 y(t)= 2.068900781342949
t= 0.7959183673469387 时
解析解求得:x(t)= 0.5499307688513946 y(t)= 2.1673384367061703 
数值解求得:x(t)= 0.5499309446566499 y(t)= 2.167338365754919
t= 0.8163265306122448 时
解析解求得:x(t)= 0.46983216919195314 y(t)= 2.26826809693694 
数值解求得:x(t)= 0.4698323509298826 y(t)= 2.2682680268561617
t= 0.836734693877551 时
解析解求得:x(t)= 0.3838692670636703 y(t)= 2.3716738002290874 
数值解求得:x(t)= 0.3838694532496656 y(t)= 2.3716737318902226
t= 0.8571428571428571 时
解析解求得:x(t)= 0.29181947099377314 y(t)= 2.477534248583156 
数值解求得:x(t)= 0.2918196618123881 y(t)= 2.4775341820833674
t= 0.8775510204081632 时
解析解求得:x(t)= 0.19345659163525064 y(t)= 2.585822582559378 
数值解求得:x(t)= 0.19345678857948362 y(t)= 2.5858225174390705
t= 0.8979591836734693 时
解析解求得:x(t)= 0.08855100315170672 y(t)= 2.6965060762808264 
数值解求得:x(t)= 0.08855120520166707 y(t)= 2.6965060133744223
t= 0.9183673469387754 时
解析解求得:x(t)= -0.02313017930517547 y(t)= 2.8095458232571393 
数值解求得:x(t)= -0.02312997178555415 y(t)= 2.8095457627403286
t= 0.9387755102040816 时
解析解求得:x(t)= -0.14182290531437092 y(t)= 2.924896412988897 
数值解求得:x(t)= -0.1418226909606244 y(t)= 2.9248963546723097
t= 0.9591836734693877 时
解析解求得:x(t)= -0.26776597737325014 y(t)= 3.04250559832613 
数值解求得:x(t)= -0.26776575610194187 y(t)= 3.042505542867204
t= 0.9795918367346939 时
解析解求得:x(t)= -0.40120082081129205 y(t)= 3.1623139535685887 
数值解求得:x(t)= -0.4012005926051197 y(t)= 3.162313901033337
t= 1.0 时
解析解求得:x(t)= -0.5423712346712355 y(t)= 3.2842545233105325 
数值解求得:x(t)= -0.5423709994286192 y(t)= 3.2842544735529384

因此其解析解为：

\[ x(t)=-sqrt(7)*exp(3*t/2)*sin(sqrt(7)*t/2)/7 + exp(3*t/2)*cos(sqrt(7)*t/2) \]

\[ y(t)=2*sqrt(7)*exp(3*t/2)*sin(sqrt(7)*t/2)/7) \]

解析解和数值解由于十分相似，在画图时不容易分辨，于是我将数值解的步长设置为0.2，解析解的步长为0.02时，其结果为：

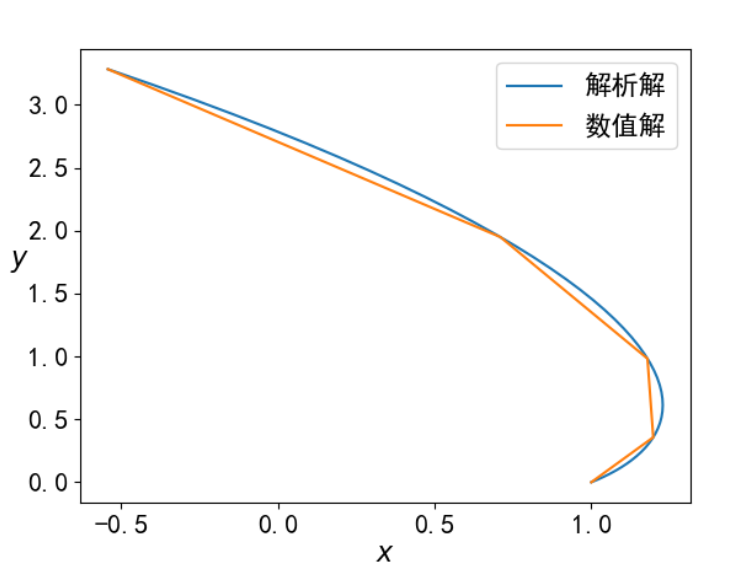
当解析解与数值解的步长相等，均为0.02时，结果如下图：

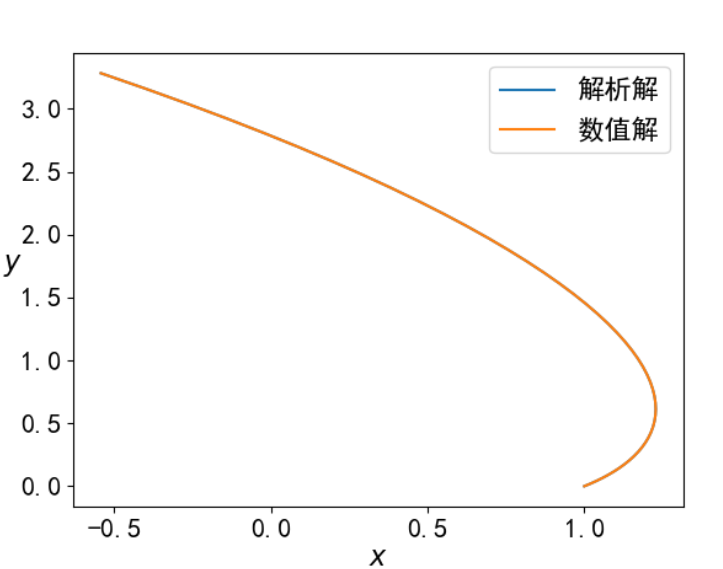
可见二者几乎完全重合。