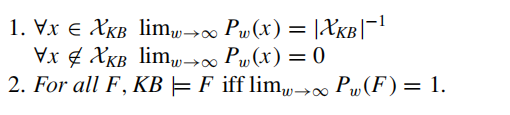Markov Logic Network-2

更新于 分类于 阅读次数： 本文字数： 2.1k 阅读时长 ≈ 4 分钟
对Markov Logic Network(2006)论文的复述

Markov logic networks 论文（Mach Learn 2006）

以下笔记仅仅是对该论文的概况复述，少有自己的思考，尚存一些疑问，如果感兴趣可以自行下载论文阅读，还可以互相交流讨论☺

论文链接

摘要

将一阶逻辑（first-order logic）和概率图（probabilistic graphical models）模型相结合成一个representation.

MLN的大致轮廓：

  1. 就是将每个formula公式都赋以权重，weights可以通过迭代求得.

  2. 还有一个constant的集合用来表示域中的实体集合，相当于上一节中的论据evidence.

Introduction

  1. 主要介绍了其发展历史，全文概览

  2. 介绍了Markov Networks，其用途主要有MCMC，Gibbs sampling，belief propagation.

  3. 介绍了First-order logic，其实就是离散数学1谓词逻辑相关内容，包括与或非，推出，相等，全称量词，存在量词。并介绍了一些专业术语ground term（不包括变量的term）ground atom值得是所有的论据都是ground term，world 指的是对于每个可能的ground atom 都为true.

Markov logic networks

一个first-order的例子：

Definition

\(L\)指的是由一对一对的\(pairs(F_i,w_i)\)组成的集合，\(F_i\)就是一阶逻辑的公式，\(w_i\)是实数，代表这个公式的权重；除此之外，还有一个有限的由常量组成的集合\(C={c_1,...,c_{|C|}}\)，代表证据.

world X概率的计算方法：

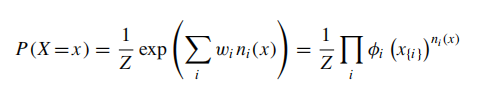
这个上一节有讲过，此处略过：

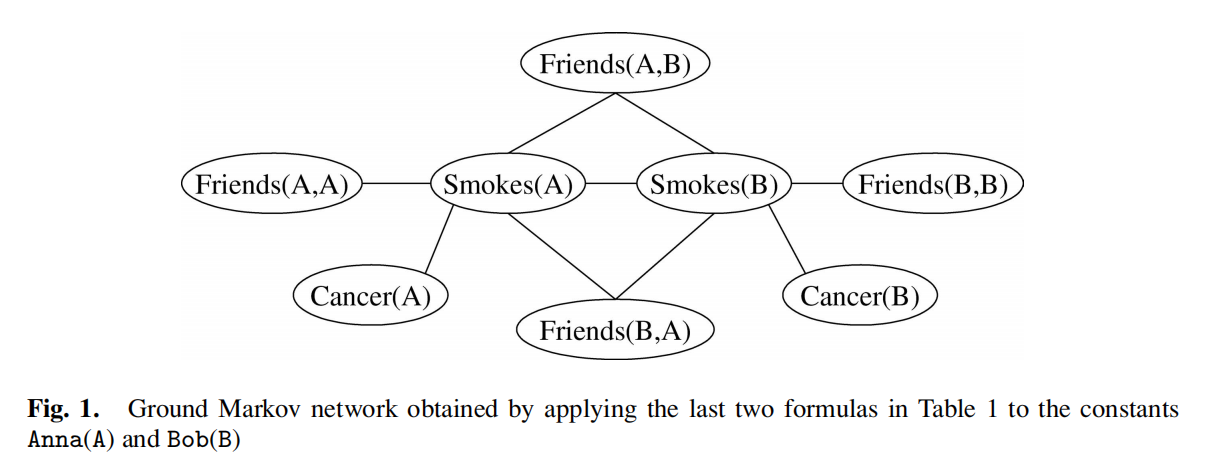
下图是Table1对应的MRF：

Assumption

接下来文章提出了三个假设，如下图所示：

  • Unique names：一对一

  • Domain closure：闭包

  • Known functions：已知的函数值是C中的元素

如何证明或者说消除上面三个假设呢?

  • 第一个假设：引入equality predicate

  • 第二个假设：引入对unknown but finite的u的distribution

  • 第三个假设：反证法

最终结论： 假设1-3在域是有限的情况下都可以被证实.

之后证明了两个proposition：

1.Every probability distribution over discrete or fifinite-precision numeric variables can be represented as a Markov logic network.

2.

Inference

如何在已知F2为真值的时候推断F1?

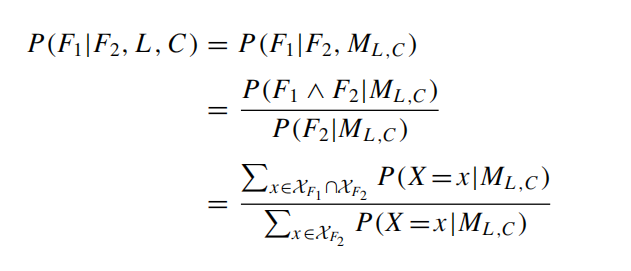
将一个KB是否包含F公式的问题转变为\(P(F|L_{KB},C_{KB,F})=1\)是否成立，至于\(P(x|M_{L,C})\)如何计算在definition部分讲过.

上述等式可以通过MCMC算法估计出来，但是速度太慢.作者提出了一个不是这么general的算法，分为两个阶段：

  1. 第一个阶段返回一个M（a ground Markov network）：

其中的MB指的是马尔科夫毯

Markov blanket （马尔科夫毯子）指某个变量，在贝叶斯新年网络中的 父节点、子节点、以及节点配偶。

U是全社会，X是个人，则MB(X)就是这个人的生活圈里

2. 第二个阶段是在M中用Gibbs sampling

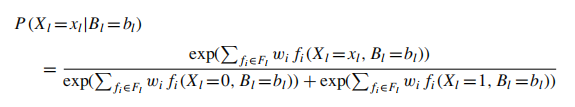
Learning

MLN的权重的学习是通过一个或多个的相关的数据库中学习的。作者基于一个假设是如果一个ground atom 不在这个database里面，则它就认为是假的.如果有n个可能的ground atom ，那么这个数据库就可以表示成一个向量\(x=(x_1,x_2,...,x_l,...,x_n)\)，如果这个atom 出现在这个数据库中则对应的xl=1，否则为零.如果第i个公式在database x中有\(n_i(x)\)的几率是正确的，那么

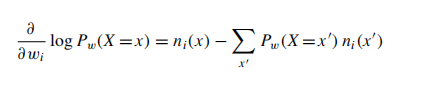
但是很显然的是通过counting来计算\(n_i(x)\)是很难实现的事情。于是引述了以下的假说：

什么是#P-complete？

也叫Sharp-P-complete问题。它和NP问题的区别就是：NP是对一个问题问有没有，#P是问有多少，因此可以看出#P比NP问题要复杂。为了在不确定数据中计算某个事件发生的概率就可能需要列出所有可能的情况，这样就会产生#P-complete问题。

为了增加效率，作者做了如下改动：

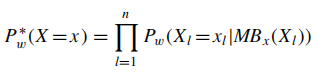
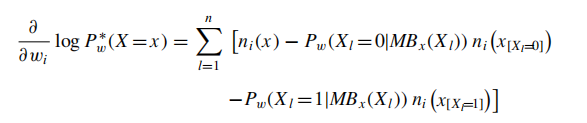
主要从以下几个方面：

  1. 第二个式子求和的时候可以忽略没在第i个公式里出现的预测函数.

  2. 对\(n_i(x_{[x_l=0]})\)的计算不会因为weight的改变而改变，且仅仅需要计算一次.

实验和结果部分

具体experiment和result可以看原论文😥

作者对只有logic或者只有概率的方法进行了对比，放个precision-recall 的结果图：

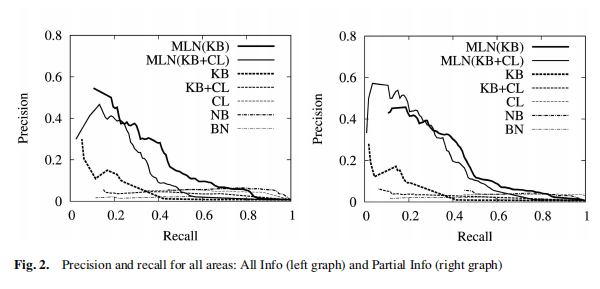
在这里介绍一下比较基础的precision和recall：

precision就是在预测为真值的情况下，实际值为true的比率；

recall就是在所有真值为true的样本里，多少样本能够被预测正确；

如果precision高，但是recall低，意味着预测一个一个准，但是还有很多没有没有被检测出来的。