SVM
类条件概率密度参数位置,形式难以确定
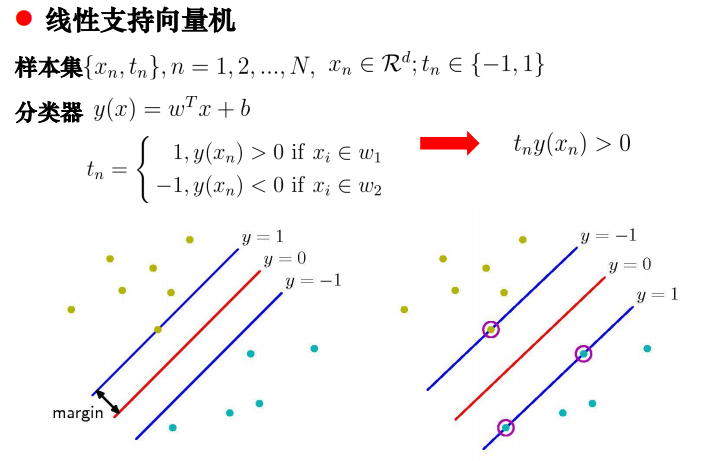
最优分类面: 将两类正确分开(error为0),且使得两侧空白区域最大(margin最大),这样可以更加鲁棒。
线性支持向量机:
是一个二分类模型,适合于中小型数据样本、非线性、高维分类问题
在说SVM之前先引入函数间隔和几何间隔两个概念:
函数间隔:
\[ \^γ=y(w^Tx+b)=yf(x) \]
函数间隔实际上是类别标签乘上f(x),可见该值永远是非负的。仔细想来,如果这个样本点不在超平面上,离得越远,f(x)的绝对值越大,而这个y标签,如果只有\({-1,1}\)中选择的话,其实相当于求f(x)的绝对值.
但是函数间隔存在一个问题是:成比例改变\(w,b\),虽然超平面没变,但是函数间隔确成倍增加.
几何间隔:
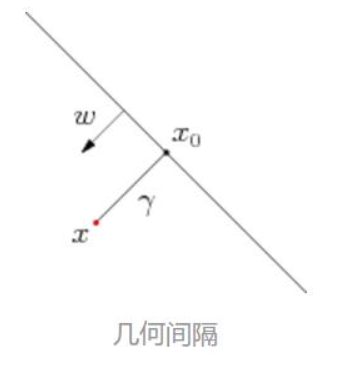
首先\(w\)是超平面的法向量,则有
\[ x=x_0+γ\frac{w}{||w||} \]
由于\(x_0\)在超平面上,所以\(f(x_0)=0\);
联立上述两式
\[ f(x)=f(x_0+γ\frac{w}{||w||})=f(x_0)+f(γ\frac{w}{||w||}) -b=γ||w|| \]
\(w^Tw = ||w||^2\)
于是有\(γ=\frac{f(x)}{||w||}\),则有,\(\~γ=yγ=\frac{\^γ}{||w||}\),可见几何间隔就是函数间隔除以w的范数。
于是问题转换为\(max(||w||^{-1})\)

凸优化和拉格朗日对偶
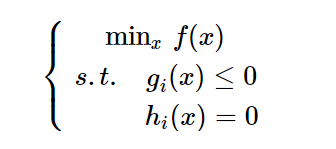
凸集:集合中的任意两点连线上的点也在该集合中,则成为凸集(凸集∩凸集=凸集;凸集∪凸集不一定是凸集)
凸优化:目标函数是凸函数,变量所属集合是凸集。对于凸优化问题来说,局部最优化解就是全局最优解。常见的凸优化问题有线性规划、半正定规划。要求\(f(x)\)是凸函数,\(g_i(x)\)是凸函数,同时\(h_i(x)\)是仿射函数(指的是线性函数,形式为\(f(x)=ax+b\))
对于一般的优化问题,对f,g,h都没有要求。
里面还有关于对偶函数、核函数(主要用于解救额线性不可分的情况)、解决线性不可分的讲述,十分详细.
SVM对应的对偶问题最终可以写成:
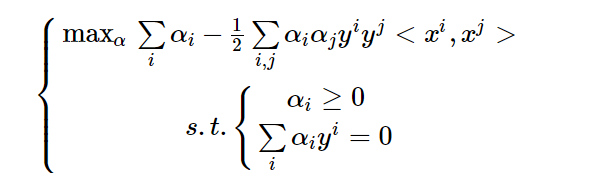
KKT条件
KKT主要用于处理非线性优化问题,是确定极值点的充要条件。
