Algorithm-DP
0-1背包问题
问题描述:
体积固定的背包,从一组存在两个属性的(体积、价格)物品中挑选,使得总体积不超过背包容量时的最大价值。
选择价格最高的、体积最小的、性价比最高的都无法保证得到最优解。
尝试蛮力枚举法(暴力出奇迹),找出价格最大的方案。
省略掉h得到简化得到的伪代码:

蛮力枚举法的复杂度高,如何优化呢?
其对应的伪代码如下:

\(P[i,c]\)可以解释为一个表格,其实就是空间换时间嘛!
其实就是自顶向下,而又自底向上的递归过程:
是否可以不递归,直接计算出\(P[i,c]\)?
妙妙子,由于\(P[i,c]=max\{P[i-1,c],P[i-1,c-v_i]+p_i\}\).所以为了确定\(P[i,c]\),需要知道其备忘录表格中上方的值和左上方的值。所以这个备忘录应该从左往右,从上往下,一次记录,最后表格右下角的值就是最终求得的值.
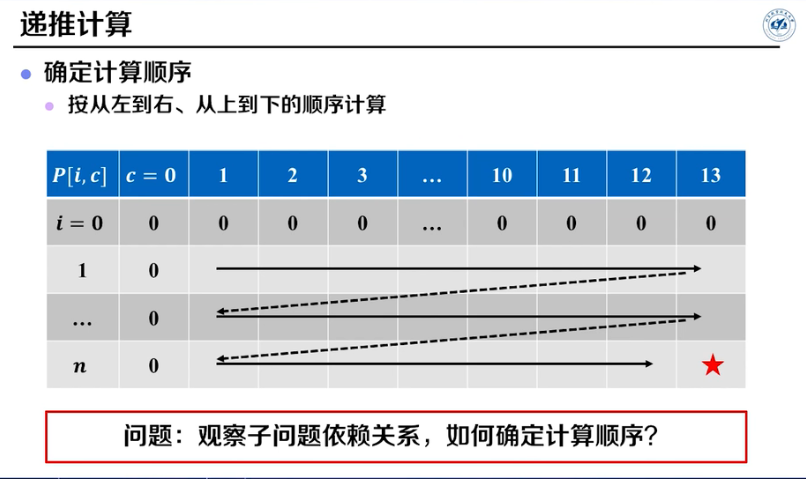
但是有一个问题是,最终得到了最优解,但是到底选择了哪些物品呢?
所以引入了一个表格\(R[i,c]=\{1,0\}\)用来记录决策过程。如果是选择了第i个物品,则为1,否则为0.
方法:从右下角往前推。 如果当前为1,则查看\(R[i-1,c-v_i]\)的位置是1还是0;否则查看\(R[i-1,c]\)的位置是1还是0,以此类推。


算法复杂度为\(O(nc)\)
什么是动态规划:就是备忘录法、递归求解。
动态规划的一般步骤
问题结构分析
递推关系建立(初始化)
自底向上计算(做好备忘录)
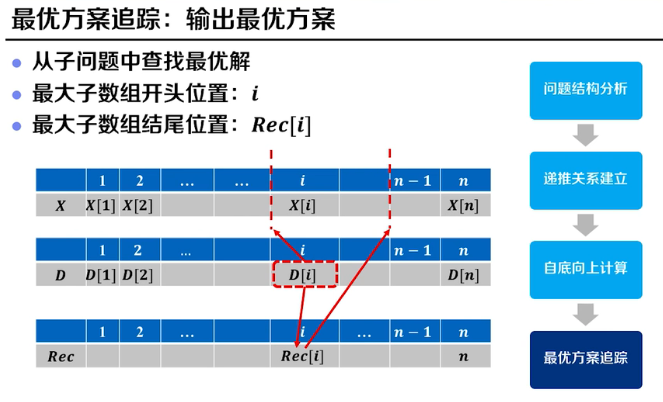
最优方案追踪(构建Rec数组)
动态规划vs分而治之
动态规划:存在重叠的子问题
分而治之:各个子问题互相独立
最大子数组问题
之前在分治算法的时候讲过。
蛮力枚举的时间复杂度为\(O(n^3)\)
分而治之的时间复杂度为\(O(nlogn)\)

动态规划算法
定义\(D[i]\)表示以\(X[i]\)开头的最大子数组和。
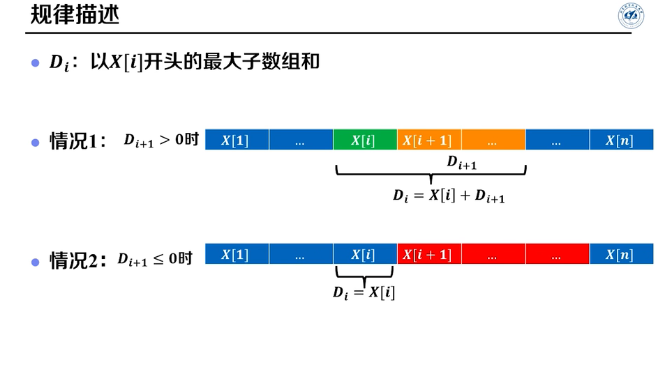
上面两种情况很显而易见,$ Rec $数组用来记录当前i的最大子数组的结束位置.
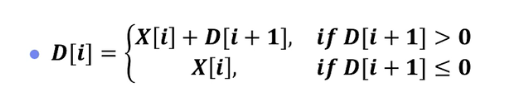
对应的伪代码为:

可见动态规划解决最大子数组问题的时间复杂度为\(O(n)\).对于找到起点和终点的方法就是先找到maxD[i],则其对应的i就是起点,Rec[i]的值就是终点.
最长公共子序列
问题描述
子序列: 一个序列去掉零个或多个字符所得的序列.
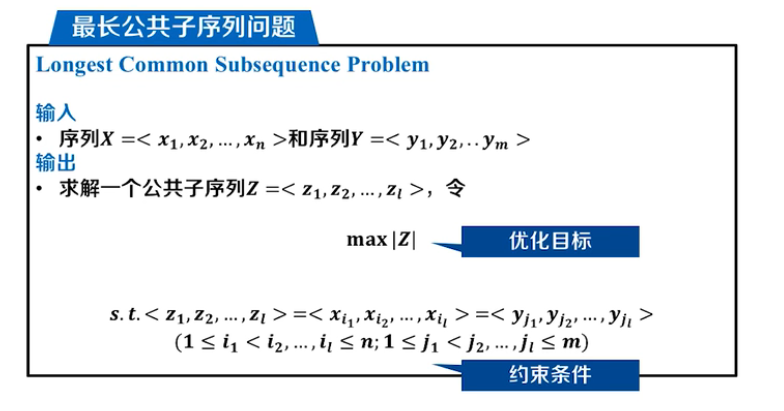
注意x序列和y序列的长度不一定相等.
一种方法也是蛮力枚举。由于长度长的子序列依赖于长度短的序列,所以一定存在重叠子问题.
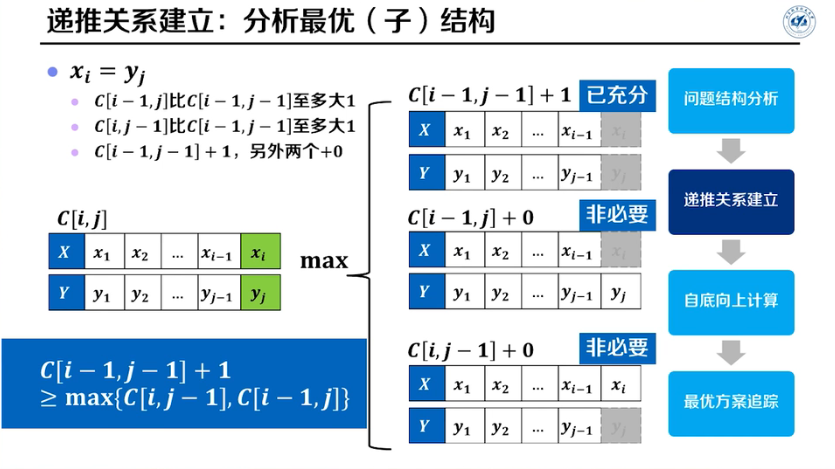
考虑末尾字符
定义\(C[m,n]\):X[1..m]和Y[1..n]的最大公共子序列的长度
两种情况:
- 末尾字符不等\(x[i-1]\neq y[j-1]\)、
\[ C[i,j]=max\{C[i-1,j],C[i,j-1]\} \]
因为末尾字符不等,所以通过减去其中一个序列的末尾字符达到相等的效果,那么相当于不相等的末尾字符在求最长公共子序列时时没有用的,舍弃就好.
那么也有可能减去一个还是不等,但是由于这是一个递归式,所以继续递归下去.
- 末尾字符相等\(x[i-1]= y[j-1]\)
\[ C[i,j]=C[i-1,j-1]+1 \]
加的1指的是最末尾的字符已经为最长公共子序列的长度贡献了1.

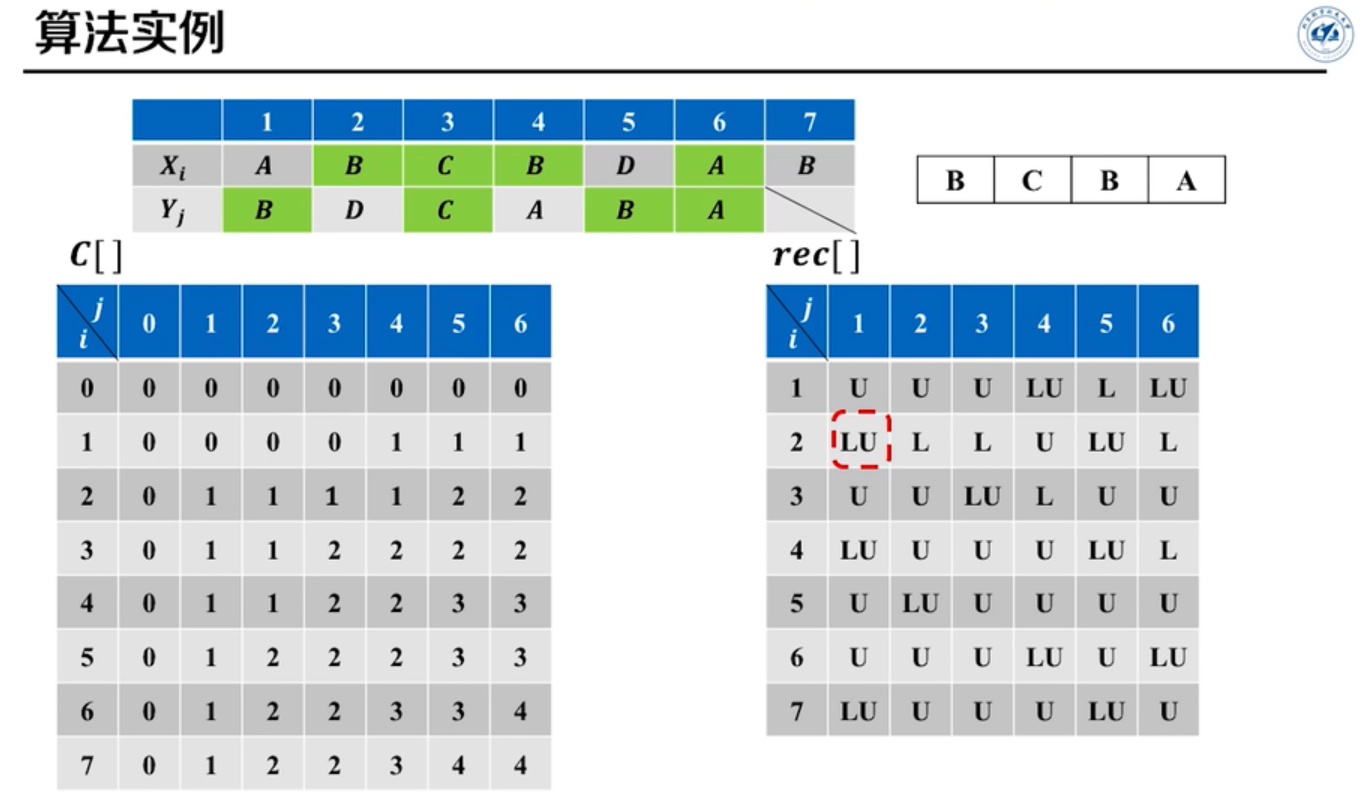
时间复杂度为\(O(nm)\)
最长公共子串
问题描述
和最长公共子序列的区别就是:子串必须连续
定义
用\(C[i,j]\)表示以\(x_i,y_j\)结尾的X[1...i],Y[1...j]的最长公共字串长度
递归公式
两种情况:
$ x_iy_j \(则\)C[i,j]=0$
\(x_i=y_j\)则\(C[i,j]=C[i-1,j-1]+1\)
PS:由于\(C[i,j]\)相当于是将所有n*m个最长公共子串长度枚举出来了,所以最终问题的最优解不是\(C[i,j]\)的右下角,而是这个表格中的最大值,应该维护两个值,分别是最优解的位置\(p_{max}\)和长度\(l_{max}\),用于最后最优解追踪,而不至于最后还要遍历表格n*m来找到最大值。其实相当于是利用动态规划的枚举方法。
最优方案追踪
记录最长公共子串末尾的位置
记录最长公共子串的长度
伪代码
初始化n,m,新建数组C[i,j],lm,pm,初始化C[i,j];(看着好像都会忘记哪些要初始化,但是把总的代码写一遍就清楚了)。
两个for循环填C[i,j]表
时间复杂度
\(O(n·m)\)
最小编辑距离
问题描述
输入:长度为n的字符串s和长度为m的字符串t
输出:一组min|编辑操作|使得s=t
定义
\(D[n,m]\):字符串\(s[1..n]\)变为\(t[1...m]\)的最小编辑距离(是一个数).
递归公式
同样考虑末尾元素:
1.删除操作:
将s的末尾删除
$ D[i,j]=D[i-1,j]+1 $(这个1代表删除操作)
2.插入操作:
将s的末尾插入一位t的最后一位,,相当于将s通过D[i,j-1]变成t[1..j-1],最后在后面插入t[j]就变成t了
\(D[i,j]=D[i,j-1]+1\)(这个1 代表最后的插入操作)
3.替换操作:
将s的最后一位替换为t的最后一位
如果\(s[i]=t[j]\)则\(D[i,j]=D[i-1][j-1]+0\)
否则,\(D[i,j]=D[i-1,j-1]+1\)(这个1代表替换最后一位)
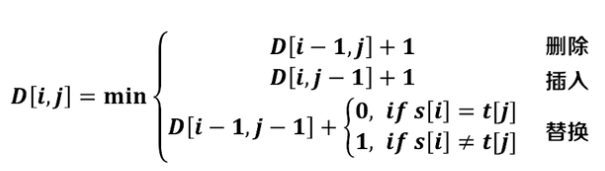
初始化
初始化\(D[i,0]=i;D[0,j]=j\)分别对应i次删除和j次插入。
最优方案追踪
D表格右下角是最优解。定义一个\(Rec[i,j]\)数组,记录子问题来源:\(L,U,LU\)分别对应删除\(s[i]\),插入\(t[j]\),用\(t[j]\)替换\(s[i]\)(或者无操作)
伪代码
初始化: n,m,新建D数组,Rec数组,初始化D和Rec数组的第一行和第一列
动态规划:

- 最优方案追踪(打印)(往往这是个递归函数):
那么,递归函数需要有结束条件,具体如下:

可以发现,是先递归调用,再输出。因为这是从后往前推导的。
时间复杂度
\(O(mn)\)
钢条切割问题(区间DP )
问题描述
钢条长度n,价格表\(p_l(1<=l<=n)\).
对于一组切割方案,求解\(max\sum_{l=1}^{m}p_{c_l}\)使得\(\sum_{l=1}^{m}c_l=n\)
定义
\(C[j]\):切割长度为j的钢条可得的最大收益
递归公式
\[ C[j]=max_{1\leq i\leq j-1}\{p[i]+C[j-i],p[j]\} \]
有最优子结构和重叠子问题,为区间动态规划,特点是取最大值max时i和j有范围,这个区间的每一种情况都要枚举,然后找出最大值。
最优方案追踪
构造\(rec[1..n]\):记录长度为j钢条的最优切割方案
不切:\(rec[j]=j\)
切割:\(rec[j]=k\)(k表格切割的长度)
从后往前,查找\(rec[j-rec[j]]\)直到为0.
伪代码
初始化:新建一维数组C[0..n],rec[0..n]
动态规划:j从1→n,内层i从1到j-1的一个for循环
最优方案追踪:
时间复杂度
\(O(n^2)\)
矩阵链乘法(区间DP)
问题描述
类似于钢条切割问题,给矩阵链加括号(分割)
定义
\(D[i,j]\):对矩阵链\(U_{i..j}\)对应的最小标量乘法次数
递推公式
\[ D[i,j]=min_{i \leq k < j}\{D[i,k]+D[k+1,j]+p_{i-1}p_kp_j\} \]
如果i = j则这个矩阵链只有一个矩阵,不存在乘法,所以D[i,j]=0
所以D表格的对角线为0,且为一个上三角(i<j)。
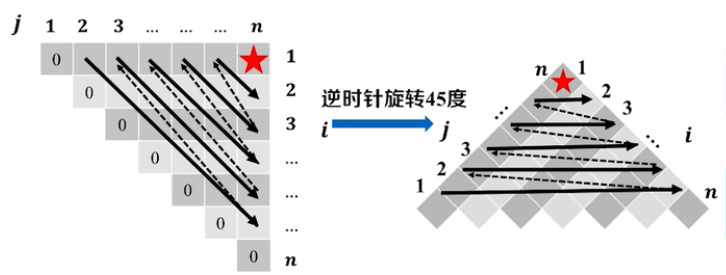
最优方案追踪
从旋转后的金字塔的尖尖所对应的最优解开始推导:如果\(rec[i,j]=k\)那么相当于是子矩阵链在k的后面切了一刀;然后再分别取查找\(rec[i,k]\)和\(rec[k+1,j]\),下图有处纰漏:

算法实例

伪代码
初始化
动态规划
最外层为矩阵链的长度,从2到n
内层嵌套的是长度为l的子矩阵链,从1到n-l+1
最内层循环是k在区间上取最小值

时间复杂度
\(O(n)\)