贪心算法

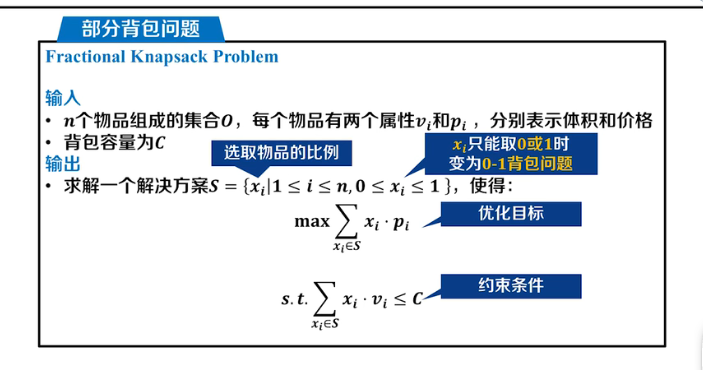
部分背包问题

输入： n个物品，每个物品又vi和pi，分别表示体积和价格，背包容量是C。

输出： 求解一个解决方案。\(S=\{x_i|0 \leq x_i \leq n \}\)，如果\(x_i\)只能选0或者1，则变成了完全背包问题。

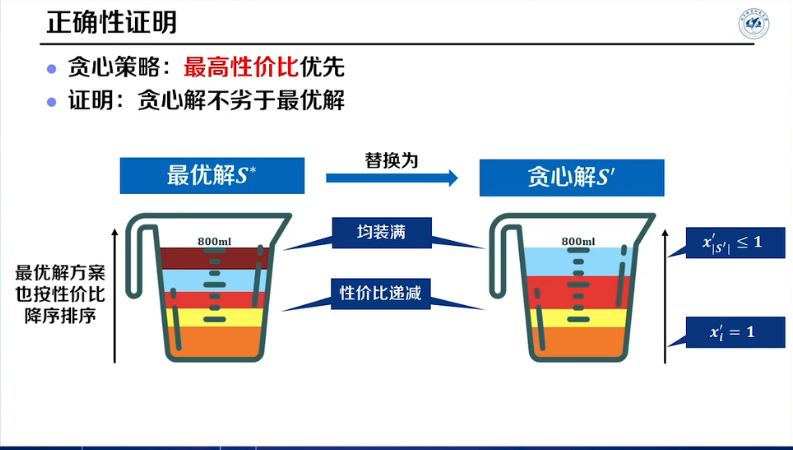
最高性价比优先

证明贪心策略是最优解，方法：替换法（假设另外存在一个最优解）

时间复杂度：\(O(nlogn)\)

---

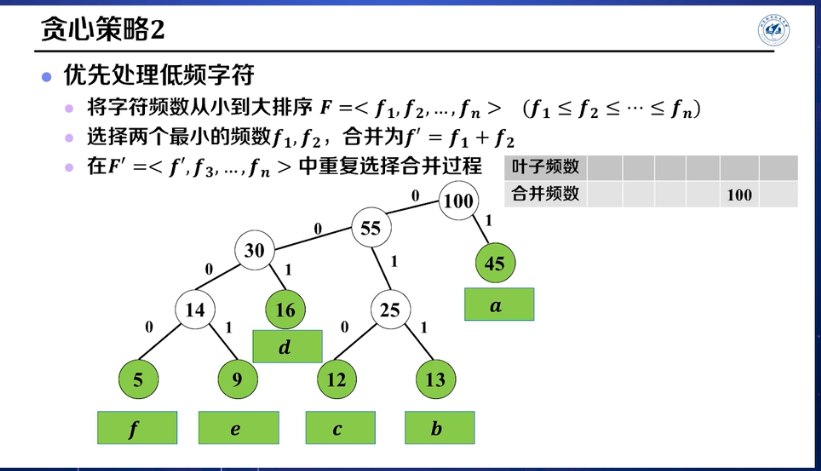
最优前缀编码问题

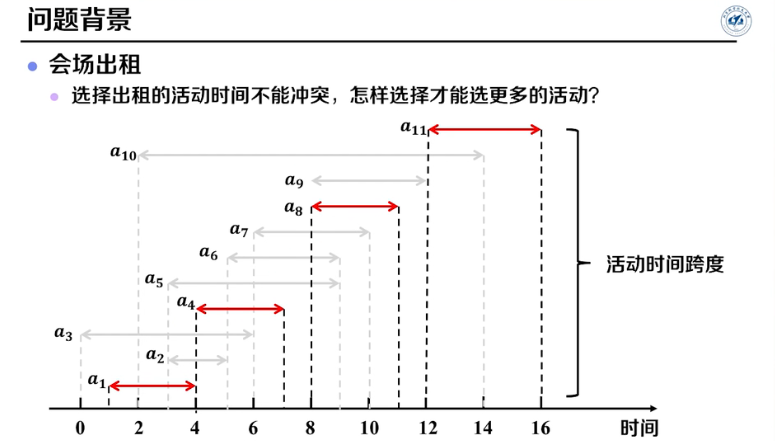
活动选择问题1

问题描述：一个会场，如何安排举办最多的活动

策略：

1. 最短活动优先

2. 最早开始活动优先

3. 最早结束活动优先

提出贪心策略→证明贪心算法就是最优解

如何证明？举反例

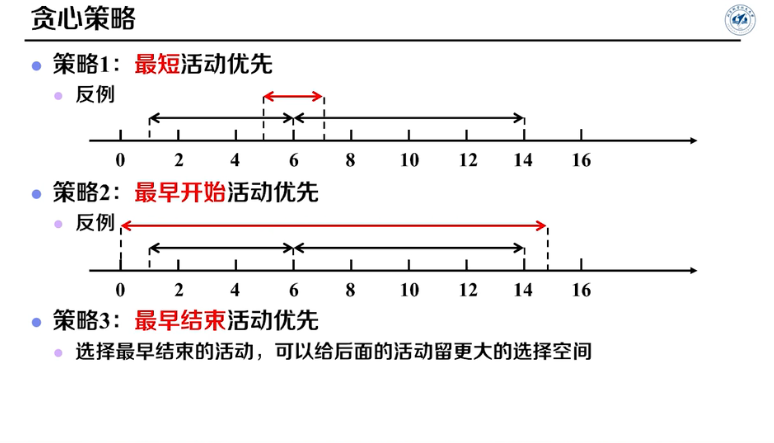
正确算法：最早活动优先

如何证明这是最优解？替换算法

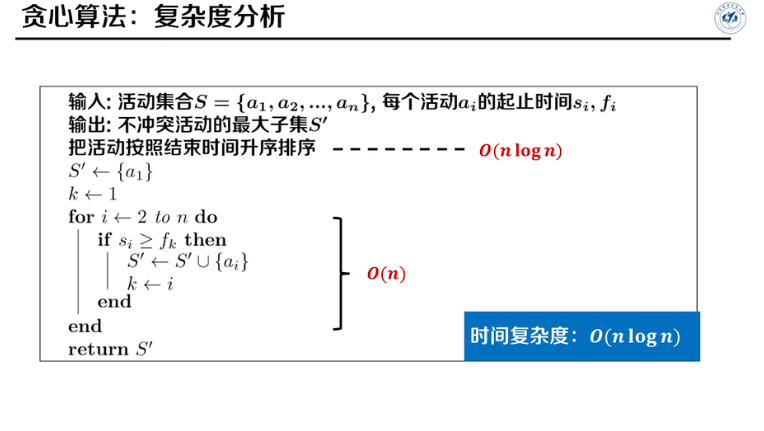
时间复杂度为\(O(nlogn)\)，仍旧为排序算法时间复杂度。

活动选择问题2

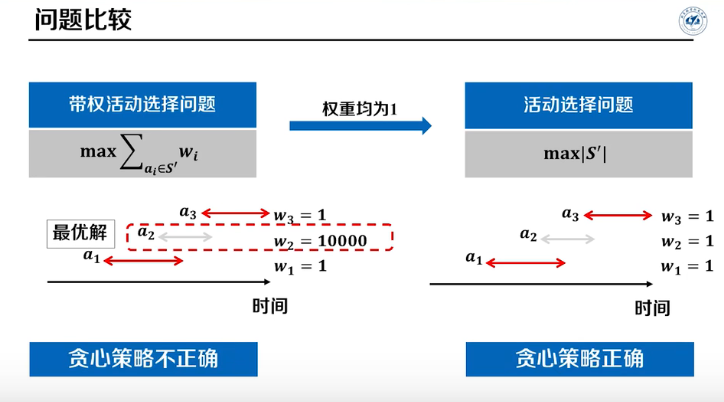
在上一个问题的基础上，使得活动的出租收益最大，相当于每个活动加了个权重。

问题定义

n个活动组成的集合\(S=\{a_1,a_2,...a_n\}\),每个活动有开始时间\(s_i\)和结束时间\(f_i\)和权重\(w_i\)。找到一个活动的子集，使得\(max\sum w_i\)，同时保证活动不能冲突。

存在重叠子问题，使用动态规划求解。

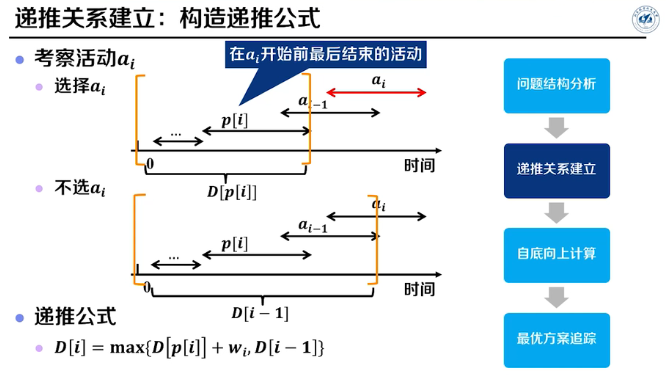
伪代码：

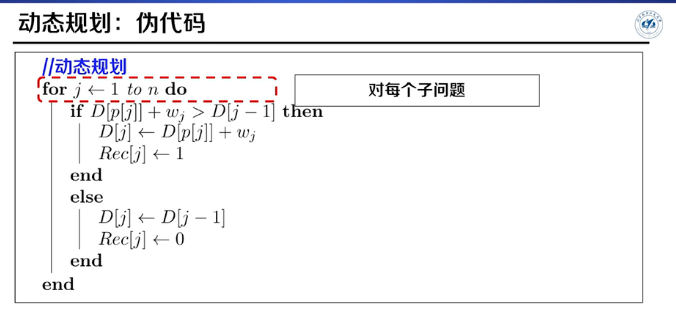
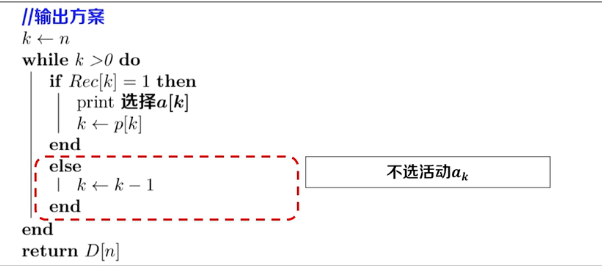
选择活动rec[i]=1，否则为0.

时间复杂度：\(O(nlogn)\)（二分查找排序时间复杂度）