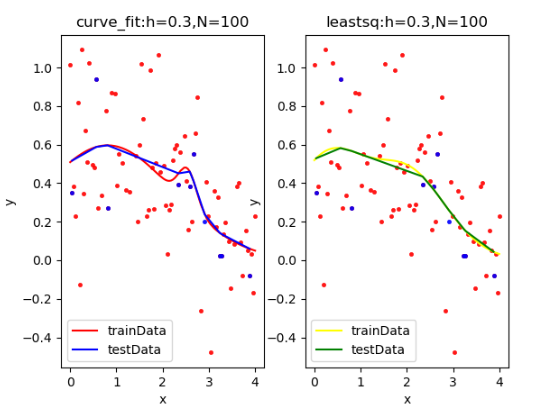
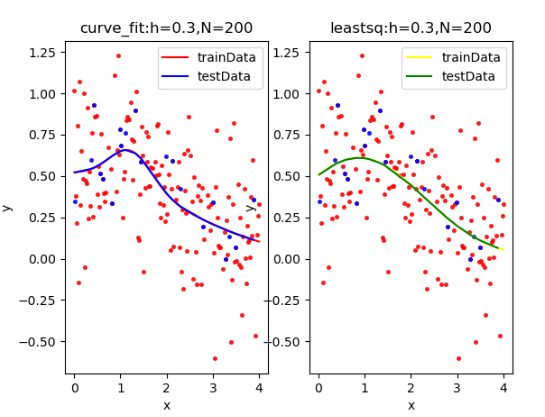
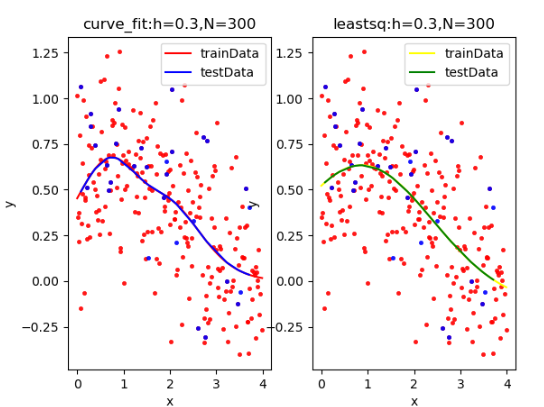
(1)第一小题
![]()
主要思路:
- 先按规定生成数据,并随机选取采样的点【设置随机种子,具有可比性】;
- 对其分别用curve_fit和leastsq进行拟合。
- 并对不同的h噪声于N采用点的数量多次拟合,得出结论。
结论:
采样点过少拟合的误差很大,选取适当的采样点以及噪声。
初始化值的影响(针对leastsq拟合)
- 迭代次数会受到影响,有些时候回出现找不到最优解的情况,即Runtime
error。
- 若全为零,则无法收敛。【不清楚具体原因】
PS:结果中拟合得到的六个数分别对应:w1,w2,a1,a2,b1,b2.
![]()
1
2
3
4
5
6
| curve_fit拟合: [2.14069954 0.09444333 0.80681967 2.54152869 1.4323823 0.19961187]
rmseTrain: 0.26232178776291626
rmseTest: 0.18205567968308098
leastsq拟合: [-3.87720452 -1.86011704 1.11854247 1.16788575 -1.04915769 0.79268749]
rmseTrain: 0.26429049990284564
rmseTest: 0.18608879973399017
|
![]()
1
2
3
4
5
6
7
| curve_fit拟合: [ 0.2408062 2.91612327 1.23109954 -0.03553431 0.45438827 2.25150756]
rmseTrain: 0.2761896128805953
rmseTest: 0.17399649531553602
leastsq拟合: [ -2.17240752 10.4348742 0.87428228 -30.76492902 -1.42103926
-0.97720794]
rmseTrain: 0.27848961091065344
rmseTest: 0.1737385154786153
|
![]()
1
2
3
4
5
6
7
| curve_fit拟合: [-0.32623604 2.15315625 1.41562053 1.12582623 0.50731064 1.0224723 ]
rmseTrain: 0.282580308684162
rmseTest: 0.31526037040858185
leastsq拟合: [ -69.65799634 -2.95866311 -109.80769737 0.86341004 168.29283316
-1.53932051]
rmseTrain: 0.2830336972922693
rmseTest: 0.3147838987502938
|
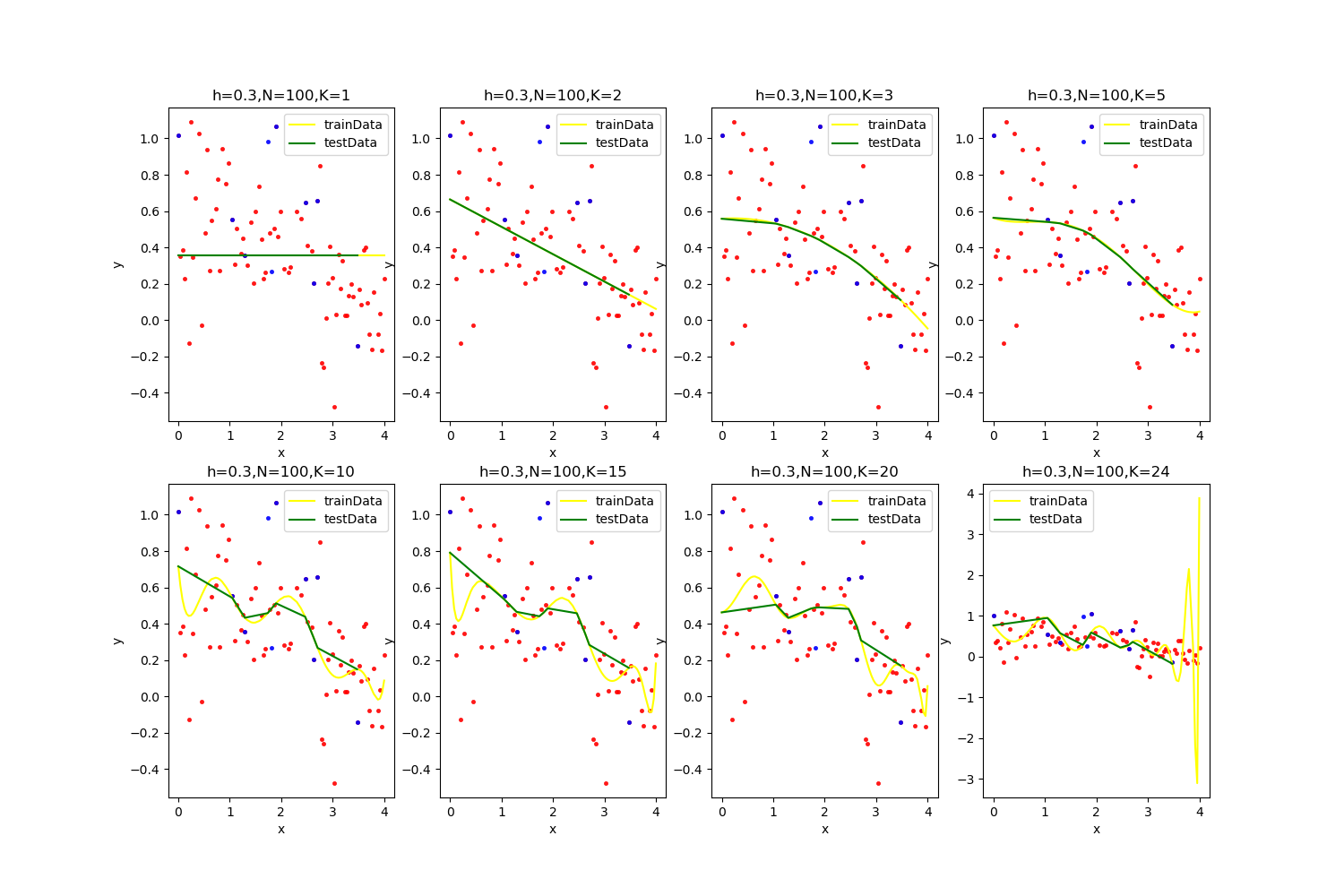
(2)第二小题
![]()
和第一小题相似的思路,进行求解。此题我用的都是leastsq进行求解。
结论:
当超参数K在超过20以后,过拟合的风险很大,在很多次情况下都出现了最后发散的情况,且通过分析结果可以发现最优解常常出现在K=15左右。
PS:结果中拟合得到的矩阵分别对应K个参数。最终求总体最优解K的时候,K遍历了1~30.。
【h=0.3,N=100】
![]()
K = 15的时候其对应的参数值为(在所有的图中最优)
1
2
3
4
5
6
| leastsq拟合: [ 7.90943650e-01 -6.07790255e+00 3.40089032e+01 -8.23686304e+01
1.05477246e+02 -7.23628142e+01 1.95321072e+01 5.57225184e+00
-4.12774052e+00 -1.00151354e+00 1.66736526e+00 -6.90740502e-01
1.45205493e-01 -1.59276567e-02 7.27046559e-04]
rmseTrain: 0.2542274166735575
rmseTest: 0.3192894171457426
|
总体最优:
1
| optimal result: trainRMSE=0.2528564533183719,K=19
|
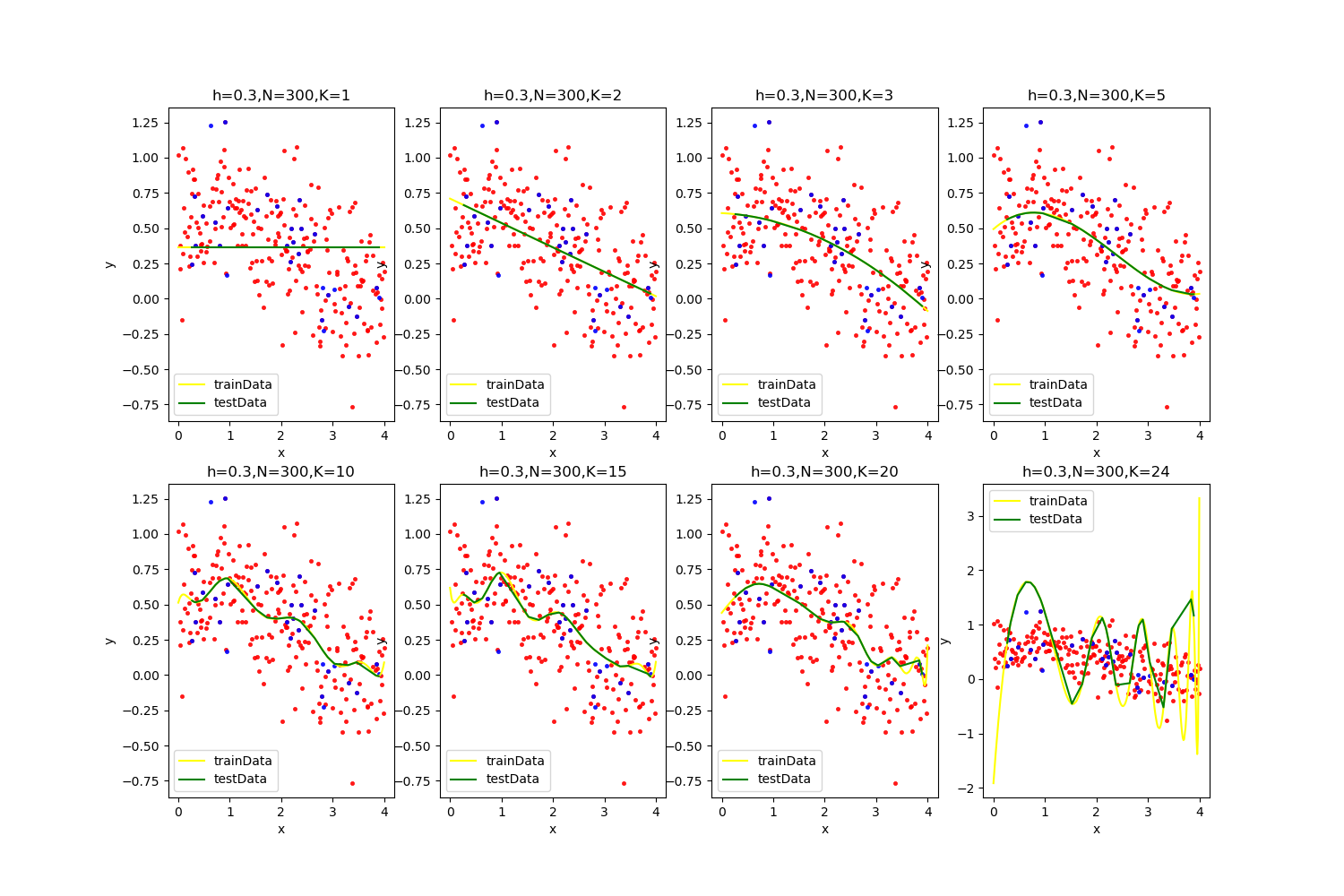
【h=0.3,N=300】
![]()
K = 10的时候最优:
1
2
3
4
5
| leastsq拟合: [ 5.12963557e-01 1.40887396e+00 -1.10781790e+01 3.22315658e+01
-4.44401511e+01 3.33253262e+01 -1.44297097e+01 3.60636603e+00
-4.83266327e-01 2.68884577e-02]
rmseTrain: 0.27528636920045013
rmseTest: 0.25770065713597756
|
总体最优:
1
| optimal result: trainRMSE=0.2812570739349669,K=13
|
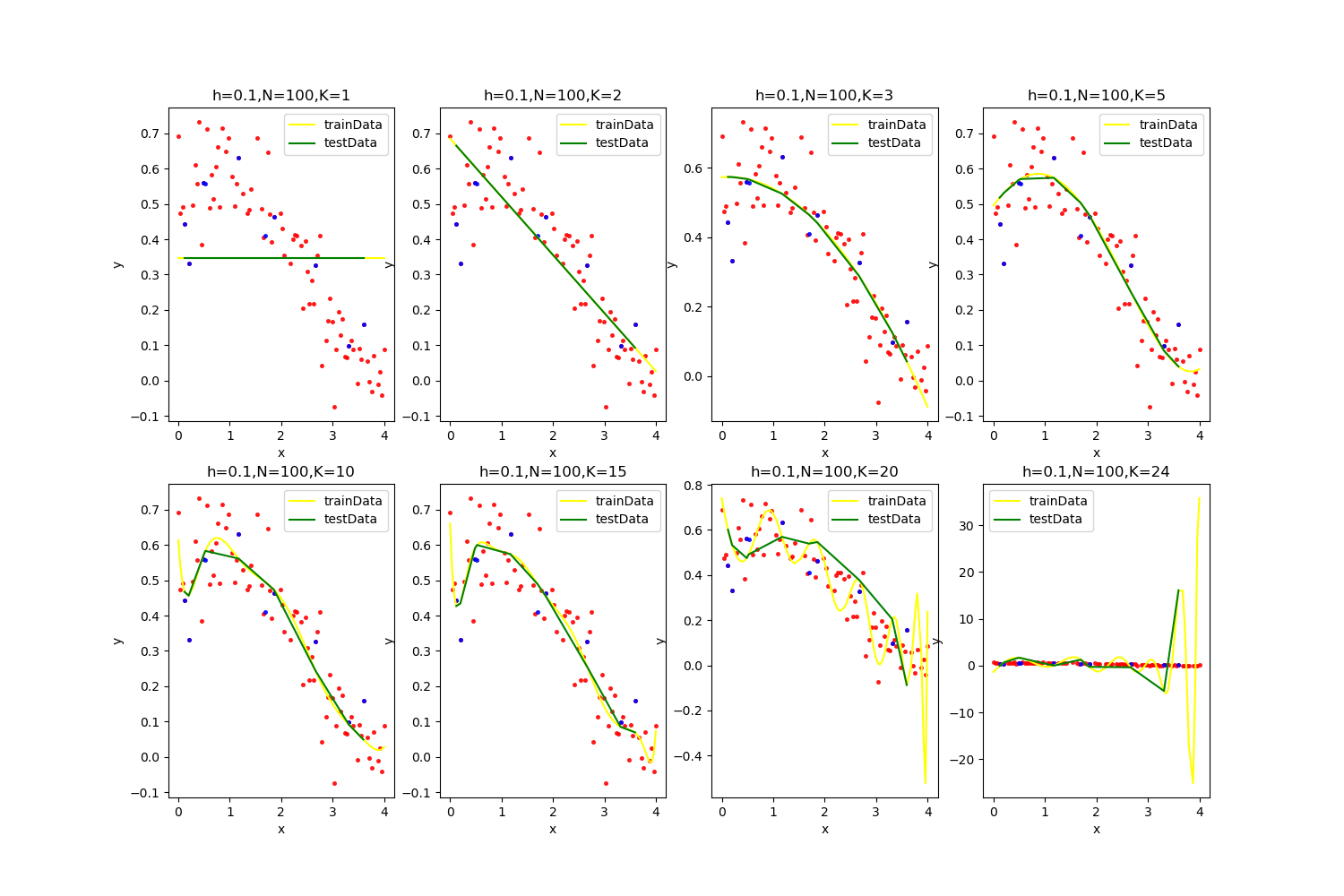
【h=0.1,N=100】
![]()
K = 15的时候最优:
1
2
3
4
5
6
| leastsq拟合: [ 6.60552408e-01 -4.02527344e+00 2.30410493e+01 -5.46928875e+01
6.69070375e+01 -4.29674450e+01 1.15661941e+01 3.10549348e-01
1.28865085e+00 -2.74964237e+00 1.70011749e+00 -5.49201917e-01
1.01626117e-01 -1.02609900e-02 4.40780742e-04]
rmseTrain: 0.07841776983416013
rmseTest: 0.06016607491515813
|
总体最优:
1
| optimal result: trainRMSE=0.07898375450702452,K=13
|
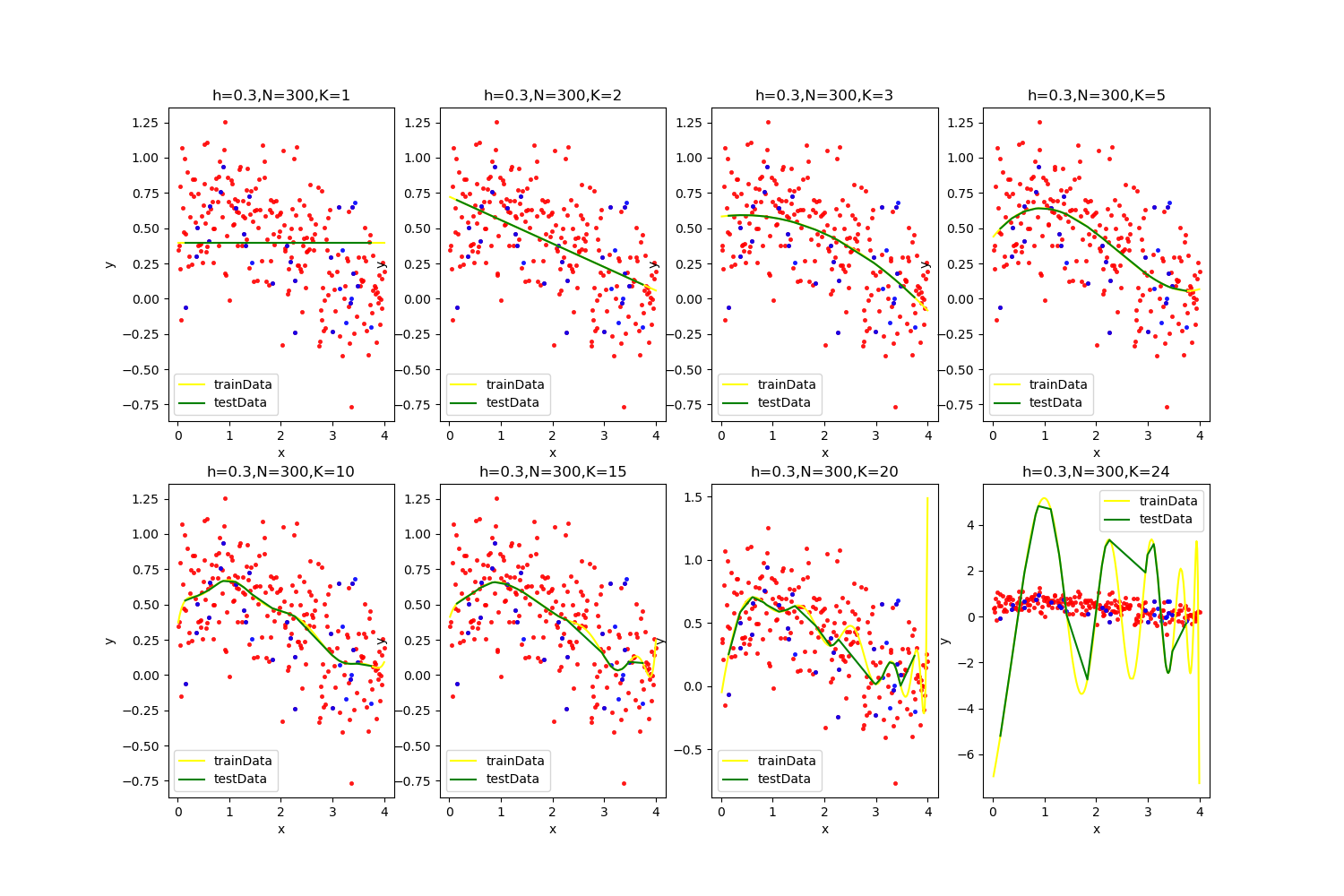
【h=0.1,N=300】
![]()
K=15的时候最优:
1
2
3
4
5
6
| leastsq拟合: [ 3.96417862e-01 1.27325013e+00 -4.73253349e+00 8.70217397e+00
-2.30403125e+00 -1.52860038e+01 2.54845292e+01 -1.89155325e+01
6.98733737e+00 -5.94285184e-01 -5.72936217e-01 2.64631449e-01
-5.28312267e-02 5.26214966e-03 -2.11610332e-04]
rmseTrain: 0.27732017692692773
rmseTest: 0.30649315630282625
|
总体最优:
1
| optimal result: RMSE=0.09689352955521495,K=15
|
(3)第三小题
![]()
这题需要注意的是其参数的个数总共应该有K
*(M+1)+2个,所以在初始化参数矩阵的时候需要设置成对应的维数,且第t[K*(M+1)], t[K*(M+1)+1]分别对应的是ai,bi.
此题遍历了K(1~5),M(1~5)。在拟合过程中,往往已经到达maxfev了还没有得到最优解,所以将maxfev设置成5000,但是到后面内存会炸...
...因此图也就只画了最优解:
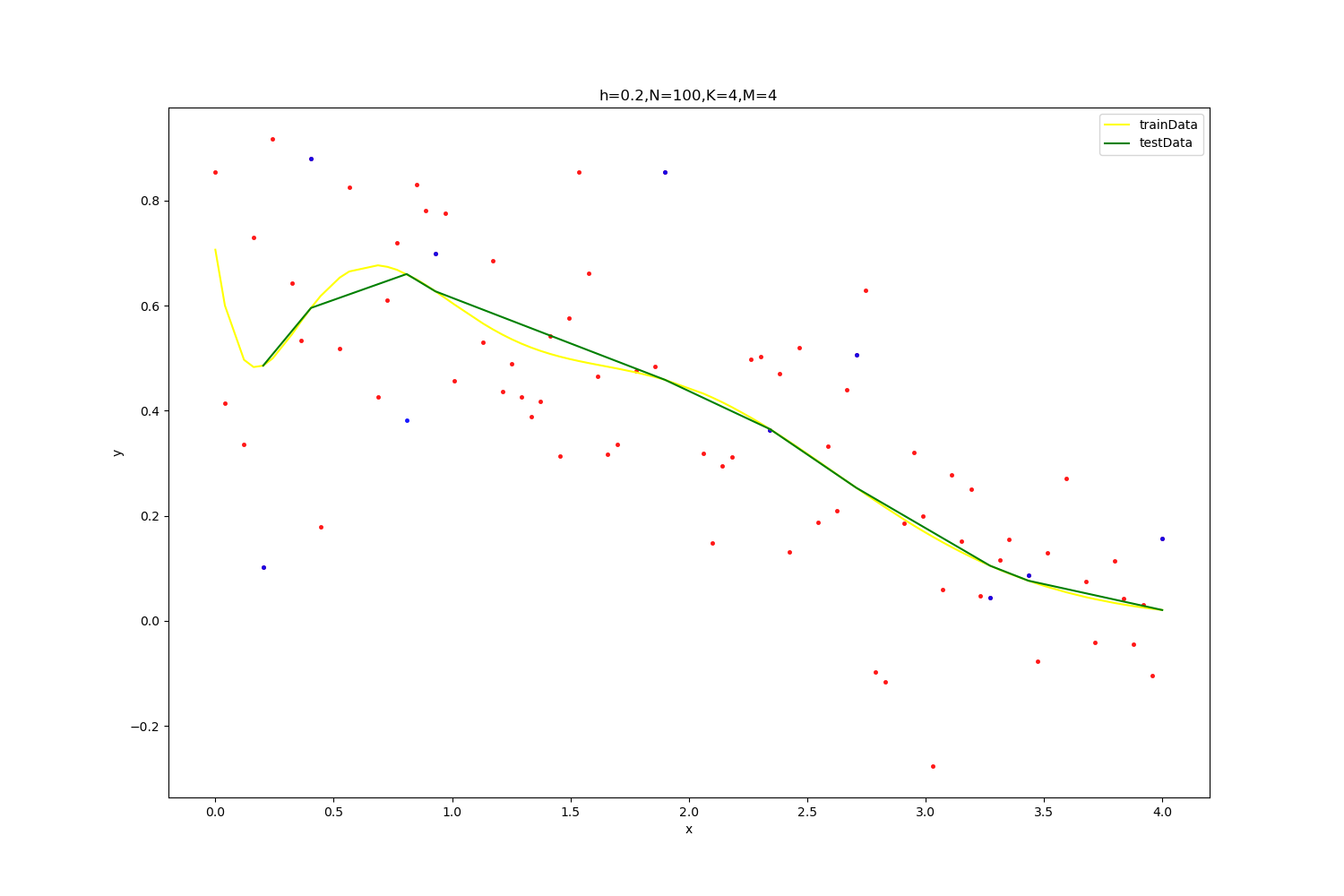
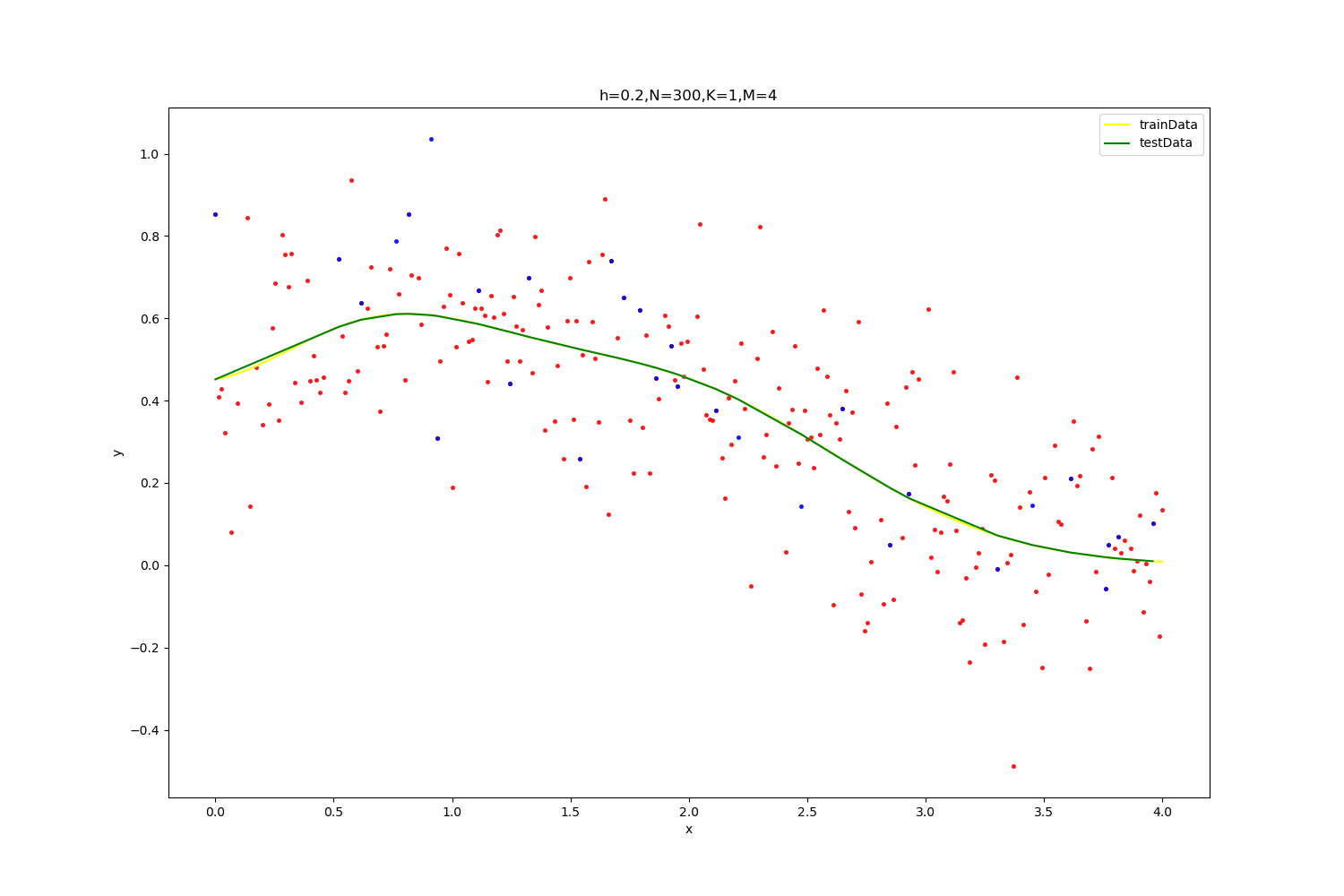
【h=0.2,N=100】
![]()
1
2
3
4
5
6
7
8
| optimal result:0.17873822672400802,K=4,M=4
拟合参数为(wij,ai,bi): [-5.23038785e+01 1.18052581e+02 5.45720103e+01 6.73970159e+01
-1.97437971e+02 -1.42252056e+02 -5.82180336e+01 -4.27695564e+01
9.18709021e+01 -1.74421852e+02 8.30403724e+01 -3.78627087e+01
2.28423291e+02 4.96400605e+01 5.97721900e+02 1.00678402e+02
1.23770905e+01 -4.21183888e+02 -3.21158789e+01 -2.94345001e+02
-2.27769369e+00 -1.29106345e+00 -8.45080274e-02 -2.97361883e-01
4.17302005e-01]
|
【h=0.2,N=300】
![]()
1
2
3
| optimal result:0.18118763840270755,K=1,M=4
拟合参数为(wij,ai,bi): [ 1.06746926 -0.23354976 2.17369779 -2.09387451 0.84513304 0.33436772
0.87670918 -0.6949209 0.5154138 -1.11487105]
|
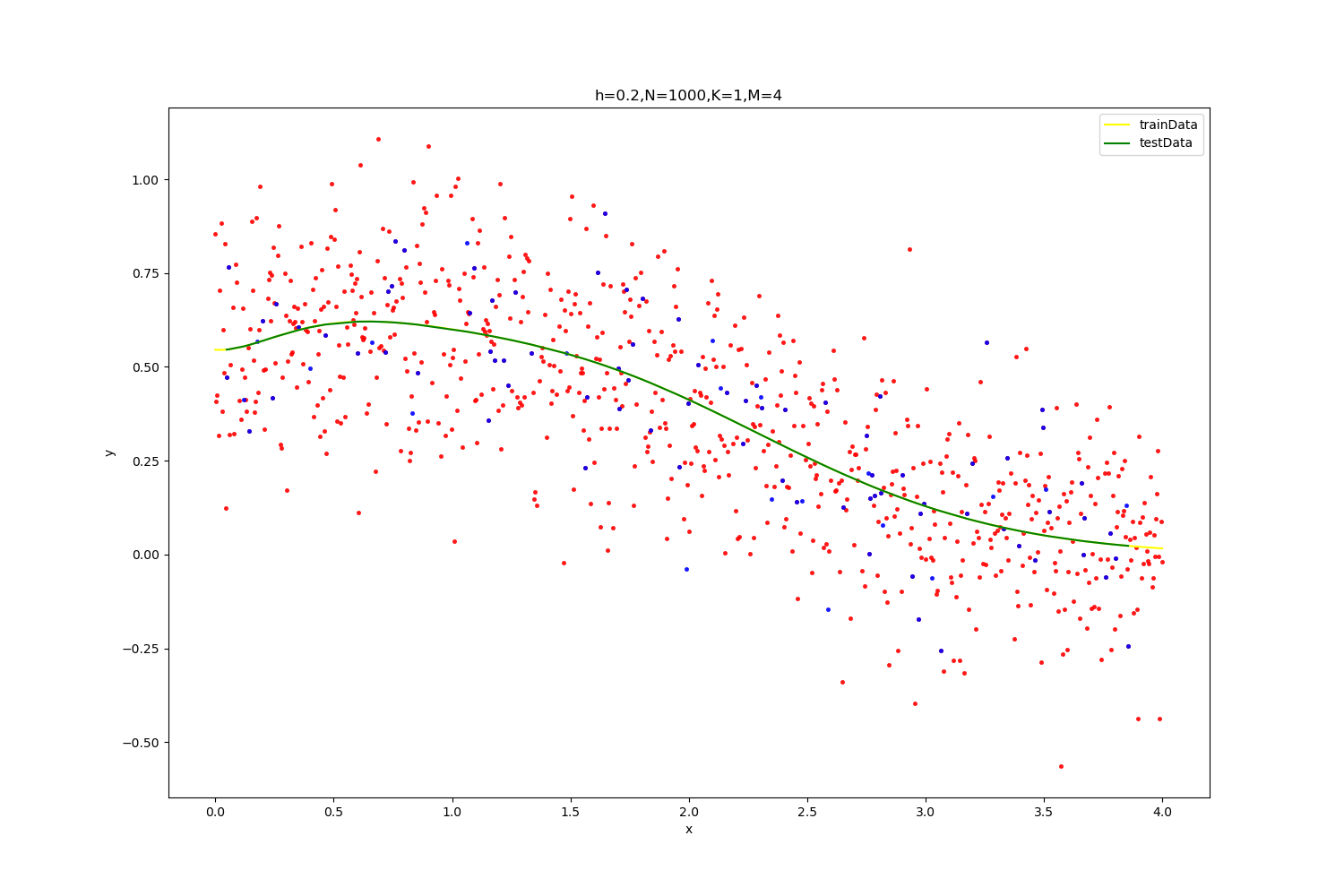
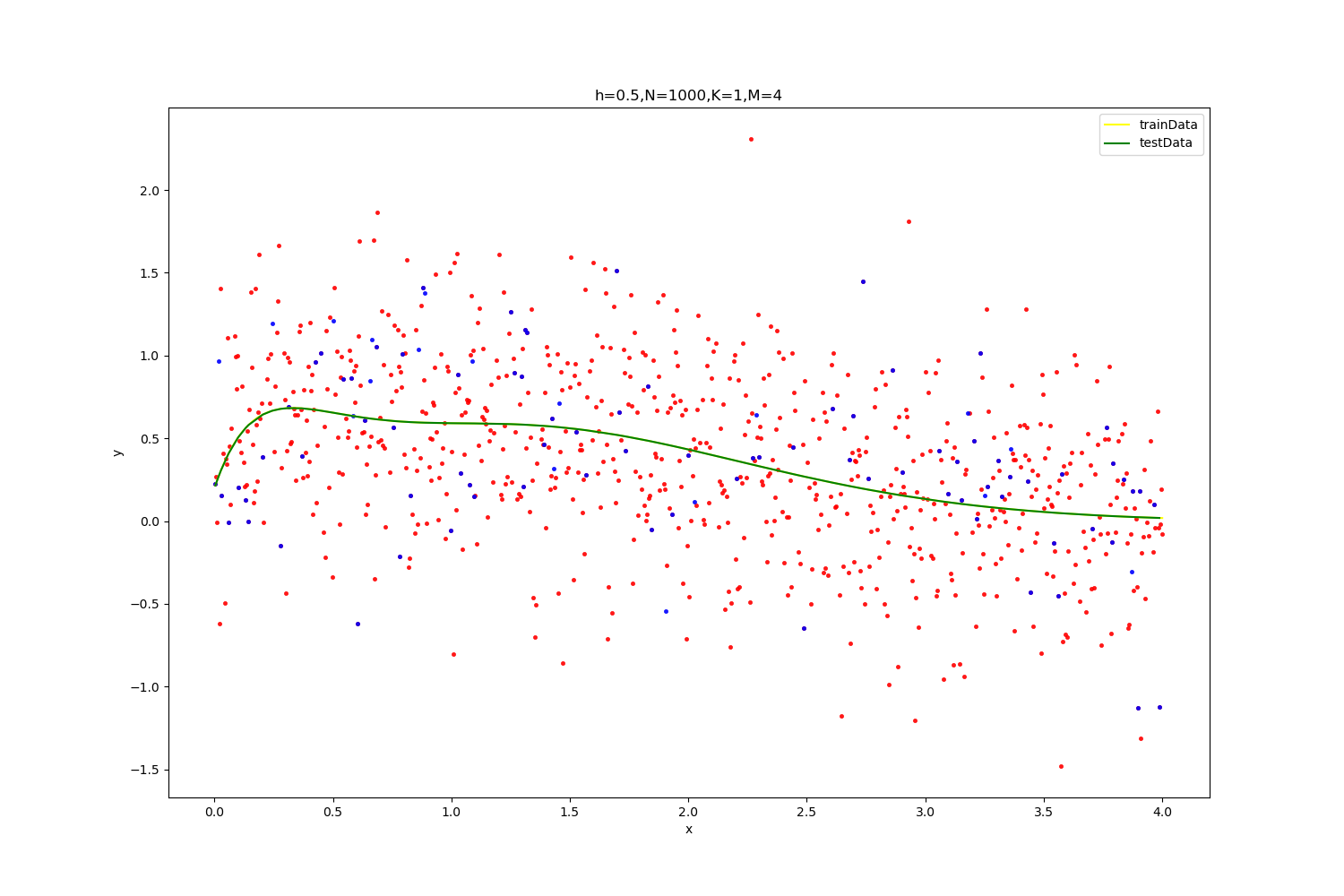
【h=0.2,N=1000】
![]()
1
2
3
| optimal result:0.19286880337431161,K=1,M=4
拟合参数为(wij,ai,bi): [ -8.09035471 -9.53448948 -29.17412061 21.14867643 -16.45334841
-2.31546224 -1.34575906 0.21633296 -1.31420103 -0.24180187
|
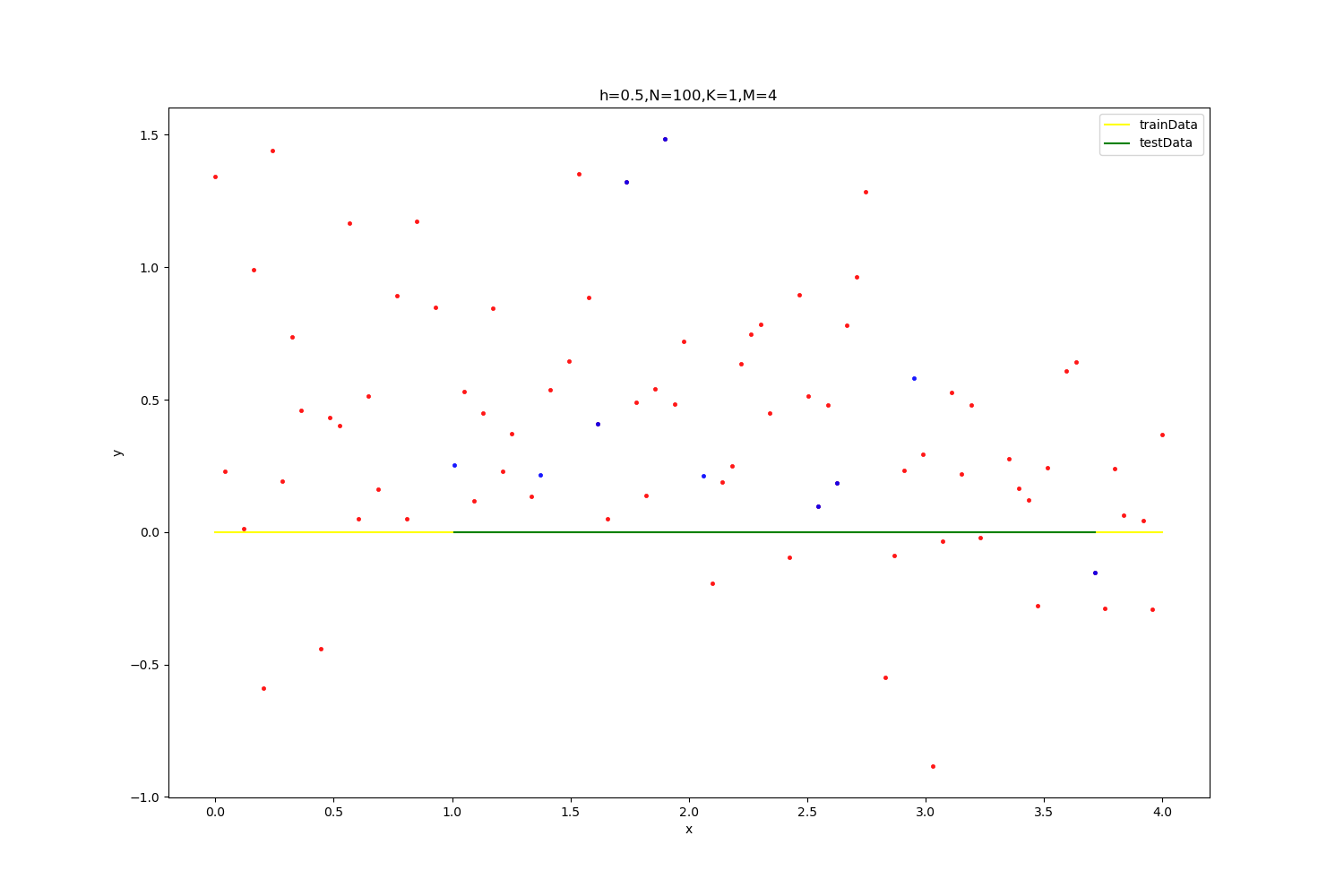
【h=0.5,N=100】
![]()
1
2
3
4
| optimal result:0.43966680795335106,K=1,M=4
拟合参数为(wij,ai,bi): [-2.67613022e+02 4.41099471e+02 -5.74683063e+02 1.02026656e+03
-5.72899644e+02 -7.29986181e+00 -7.36054845e-01 1.39984394e+00
-7.81911683e-01 -4.37508983e-01]
|
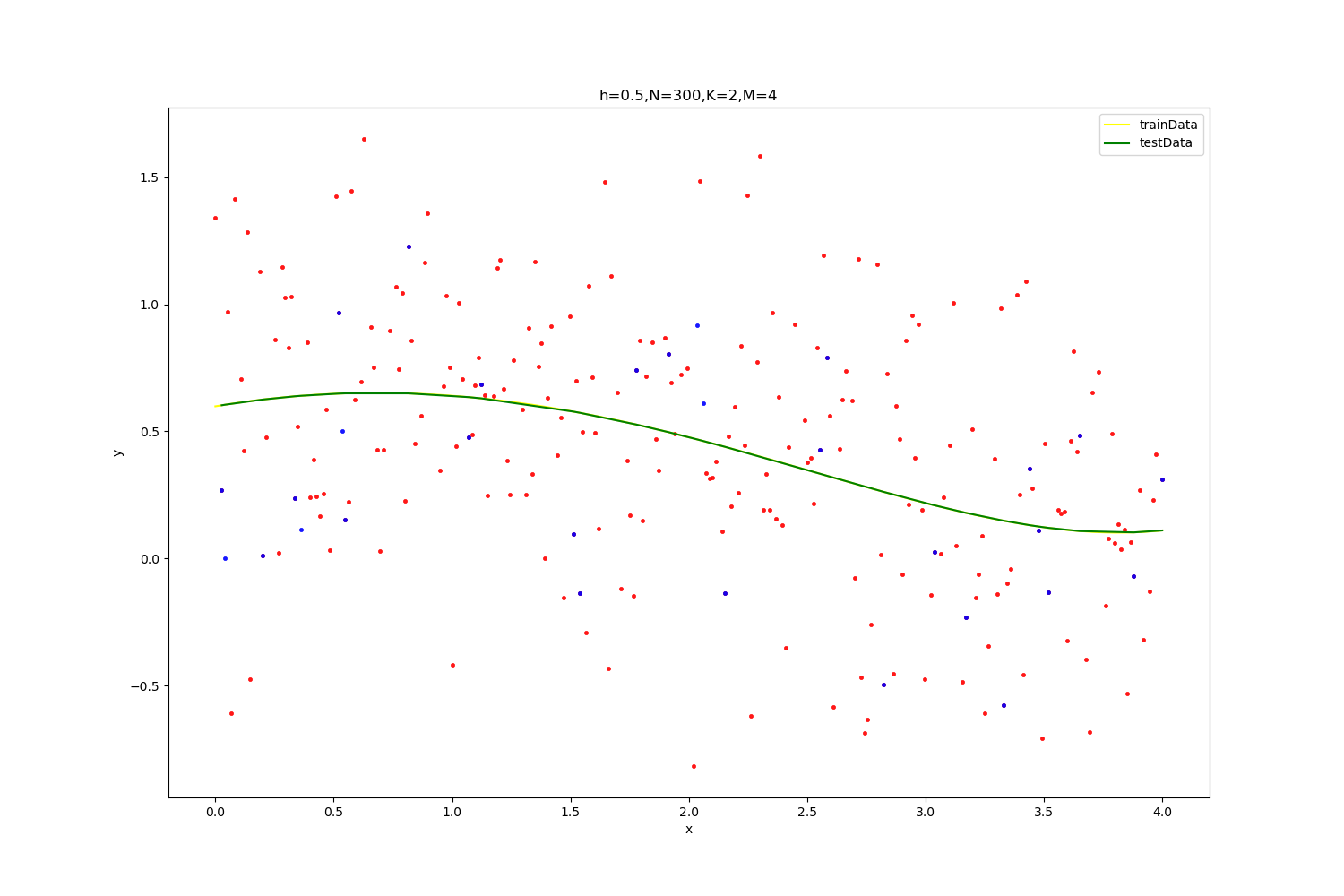
【h=0.5,N=300】
![]()
1
2
3
4
| optimal result:0.4681035667876177,K=2,M=4
拟合参数为(wij,ai,bi): [299.78797515 28.87566283 -49.79908816 8.91462082 -1.8215882
298.53012447 27.46238369 -81.20025633 9.62740177 2.38413704
39.09115188 15.30831486 1.46089238 0.5924728 1.19783084]
|
【h=0.5,N=1000】
![]()
1
2
3
4
| optimal result:0.489592101202918,K=1,M=4
拟合参数为(wij,ai,bi): [-7.69013200e+03 -1.79048782e+05 2.63642290e+05 -2.51621936e+05
4.04690946e+04 -1.03663719e+01 -2.47965800e+00 2.16332958e-01
-1.31420103e+00 -2.41801865e-01]
|
结论:
当采样点高到1000个的时候,拟合曲线极其平滑,且K与M大多分别取在1和4附近,能得到最优解。噪声越高,也会使得RMSE变高,精度下降。
(4)第四小题
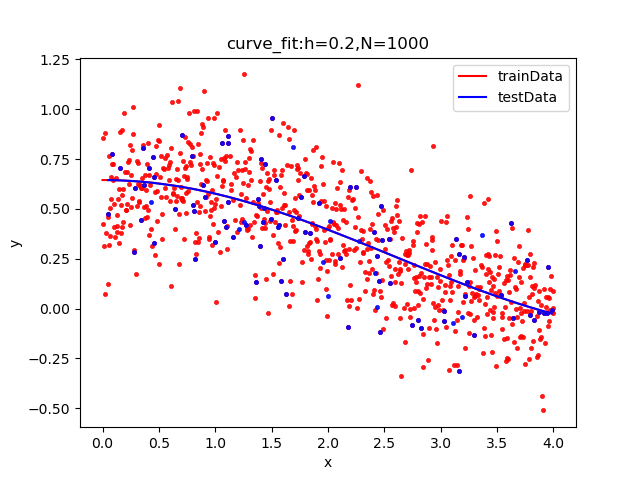
![]()
噪声和采样点数的影响与前三小题类似。
![]()
curve_fit拟合对应的分别为a,b,c.
1
2
3
| curve_fit拟合: [0.38197691 0.60783395 0.26275028]
rmseTrain: 0.20056951038840645
rmseTest: 0.20317551977817713
|
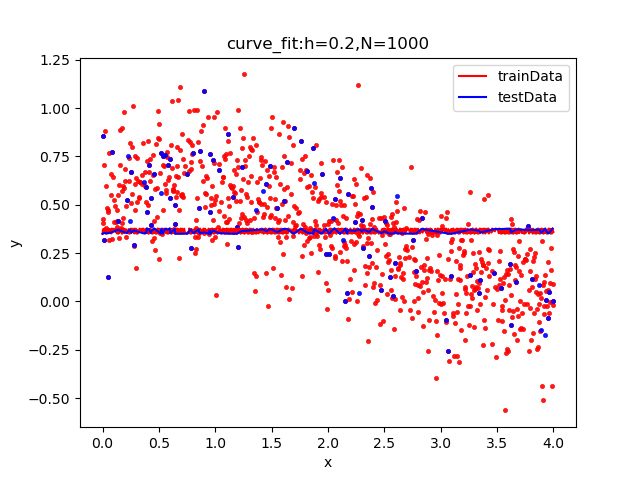
若将b设置成10000,则有
![]()
1
2
3
| curve_fit拟合: [-0.01377563 0.36384608]
rmseTrain: 0.2993405343270346
rmseTest: 0.29352661180630557
|
由结果知:a = -0.01377563,c =
0.36384608.且RMSE在测试集和训练集上均增加。
(5)第五小题
![]()
对于(2)-(4)的三种模型,选取验证集上RMSE最小的,计算对应模型在测试集上的RMSE:
设置的h=0.3,N=500
结果如下:
1
2
3
4
5
6
7
8
9
10
11
12
| -------Model1------
rmseTrain: 0.290052586241592
rmseCheck: 0.27685893060069033
rmseTest: 0.29482945312589964
-------Model2------
rmseTrain: 0.5209075125582714
rmseCheck: 0.509217190063768
rmseTest: 0.5711414271483303
-------Model3------
rmseTrain: 0.2961863452096645
rmseCheck: 0.2863578974670555
rmseTest: 0.3048874158254555
|
可见第二小题对应的模型比第四小题的模型略胜一筹,第三小题的模型相对误差较大。