非线性规划、二次规划

更新于 分类于 阅读次数： 本文字数： 3.1k 阅读时长 ≈ 5 分钟
数学建模-非线性规划

二次优化、凸优化和非线性规划

非线性规划

目标函数或者约束条件的表达式中至少有一个非线性函数。

上述为非线性规划的一般形式， 还有向量形式。

  • 可行解的集合叫做可行域。
  • 区分全局最优解和严格全局最优解
  • 区分局部最优解和严格局部最优解

凸优化：局部最优解就是全局最优解【eg.线性规划、二次规划】

二阶偏导数矩阵： 称为\(f(x)\)的Hesse矩阵

无约束非线性规划局部最优解

  • 必要条件：f(x)具有连续的一阶偏导数，且其一阶偏导数等于零。
  • 充分条件：f(x)具有连续的二阶偏导数，且一阶导为零，二阶导正定。

【尽可能将非线性转换为线性，约束问题转换为无约束问题。】

有等式约束的非线性规划的Lagrange乘子法

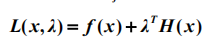
拉格朗日的意义在于将问题转化为无约束问题求解，因为将约束都加入到了L函数中。

然后等式两边求导等于零：

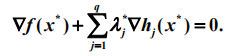
有约束非线性规划的罚函数法

由于一般形式的有约束非线性规划都会有不等式的约束，所以拉格朗日无效。

代表性：外点法

不等和相等其实可以对应，在于什么函数让两者对应起来，这个函数就是max{}.

凸函数和凸集的定义

对于n维欧氏空间里的点集，对于这个空间中的任意两点x1和x2，其连线上的所有点【\(ax_1+(1-a)x_2\)】也属于这个空间，那么就成这个点集时凸集。

任何两个凸的交集也是凸集。

有限个凸函数的飞赴线性组合也是凸函数。

凸函数的充要条件

  1. 一种普通说法
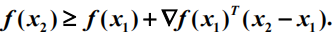
  1. f(x)的Hesse矩阵处处半正定。
  2. f(x)的Hesse矩阵都是正定的 → 严格凸函数。

【正定：其矩阵特征值全为正】

什么叫凸优化/凸规划【凸优化的判定】

对于前面提出的非线性规划，f(x),g(x)是凸函数，h(x)是线性函数。

关于是否是凸优化的求解方法

例题1

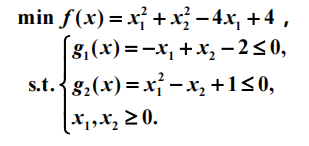
STEP1：判断是否是凸优化

方法：计算f(x)和g(x)的Hesse矩阵，如果都是大于等于零，且约束条件都是线性的。

STEP2：凸优化求解

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import cvxpy as cp

x=cp.Variable(2,pos=True)
obj=cp.Minimize(sum(x**2)-4*x[0]+4)
con=[-x[0]+x[1]-2<=0,
     x[0]**2-x[1]+1<=0]
prob = cp.Problem(obj, con)
prob.solve()
# prob.solve(solver='GUROBI')
print("最优值为:",round(prob.value,4))
print("最优解为：\n", np.round(x.value,4))

KKT条件

【在SVM介绍过相关内容】

是非线性规划的必要条件，是凸优化的充要条件。

对于凸优化问题，若x满足KKT条件，则x必为凸优化的局部最优解，进而为全局最优解。【一般非线性规划只能找到局部最优解，于初始值相关】

实际应用题解答方法

主要就是要写出这些变量和假设，以及目标函数是什么。

最后发现f是凸函数，于是只需要求其一阶偏导=0就能求出最优解。

灵敏性

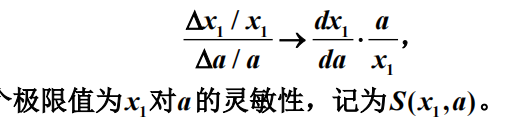
注意在求dy/da的时候，可以用链式法则。

1
2
3
4
5
6
7
8
# 使用plt.subplot来创建小图. plt.subplot(221)表示将整个图像窗口分为2行2列, 当前位置为1.
plt.subplot(221)
# plt.subplot(222)表示将整个图像窗口分为2行2列, 当前位置为2.
plt.subplot(222) # 第一行的右图
# plt.subplot(223)表示将整个图像窗口分为2行2列, 当前位置为3.
plt.subplot(223)
# plt.subplot(224)表示将整个图像窗口分为2行2列, 当前位置为4.
plt.subplot(224)

二次规划

其一般形式为：

二次规划模型是一种特殊的非线性规划模型，其Hesse矩阵为

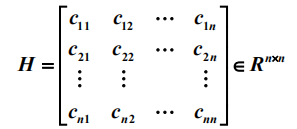
如果H正定，则模型为凸二次优化，凸二次规划局部最优解就是全局最优解。

例题2

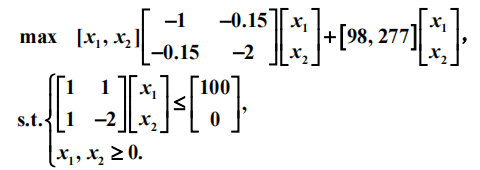
总结： 二次规划相对于普通的非线性优化的特点：其目标函数f(x)没有0次项。

【注意！！如果是min f(x)则不是凸优化！！】

【*****计算的是x'W***x的值】

a.shape[0] 行数大小；

a.shape[1] 列数大小。

1
2
3
4
5
6
7
8
9
10
11
12
13
c2 = np.array([[-1, -0.15],[-0.15, -2]])
c1 = np.array([98, 277])
a = np.array([[1, 1], [1, -2]])
b = np.array([100, 0])
x = cp.Variable(2, pos=True)
obj =cp.Maximize(cp.quad_form(x,c2) + c1 @ x)
# obj =cp.Minimize(cp.quad_form(x,c2) + c1 @ x)
con = [ a @ x <= b]
prob = cp.Problem(obj, con)
prob.solve()
# prob.solve(solver='GUROBI')
print('最优解为：', np.round(x.value,4))
print('最优值为：', round(prob.value,4))

投资组合问题

a.mean(axis=0)计算每一列的平均值；

a.mean(axis=1)计算每一行的平均值。

1
2
3
4
5
6
7
8
9
a = np.loadtxt('data6_4.txt')
mu = a.mean(axis=0)   #计算年平均收益
F = np.cov(a.T)       #计算协方差矩阵
x = cp.Variable(3, pos=True)
ob1 = cp.Minimize(cp.quad_form(x,F))
con1 = [ mu @ x >= 0.15,
        sum(x) == 1 ]
prob1 = cp.Problem(ob1, con1)
prob1.solve()

一般线性规划

由于不是凸优化，*所以不能使用cvxpy来求解，需要用*scipy.optimize的minimize来求解。

ps:约束条件大于等于零.

例题3

不是凸优化，因为h(x)不是线性的.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
from scipy.optimize import minimize

obj=lambda x: sum(x**2)+8
def constr1(x):
    x1, x2, x3 = x
    return [x1**2-x2+x3**2,
            20-x1-x2**2-x3**2]
def constr2(x):
    x1, x2, x3 = x
    return [-x1-x2**2+2, x2+2*x3**2-3]
con1={'type': 'ineq', 'fun': constr1}
con2={'type': 'eq', 'fun': constr2}            
con=[con1, con2]  #构造全部约束条件
bd = [(0, np.inf) for i in range(3)]
res = minimize(obj, np.random.randn(3), constraints=con, bounds=bd)
print(res)  #输出解的信息

注意：如果用sympy.optimize.minimize求解，则con是ineq的时候保证是大于等于零的。

例题4

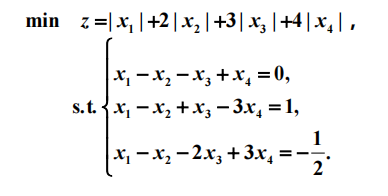
由于f(x)和g(x)是凸函数，且h(x)是线性的，所以是凸优化问题，可以用cvxpy求解。