中风预测

更新于 分类于 阅读次数： 本文字数： 5.7k 阅读时长 ≈ 10 分钟
决策树和lstm解决不平衡数据的二分类问题

个人作业

数据预处理

读入数据

1
2
train_data = pd.read_csv('./train.csv', encoding='ISO-8859-1')
len_train_data = len(train_data)

数据数字化

使得未用数字标识的性别、是否结婚、工作、居住地、是否抽烟用数字表示。

由于bmi指数有上百条数据为空，所以这里的处理是求取bmi均值，替代空值【原本的处理方式是将bmi为空值的数据丢弃，但是由于标签为1的稀疏性，最后的预测结果很差，所以最后还是将bmi为空值的数据用均值替代】。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
for i in range(len_train_data):
    entity = train_data.loc[i]
    if math.isnan(entity['bmi']):
        entity['bmi'] = bmiAve
    label_list.append(entity['stroke'])
    del entity['id']
    del entity['stroke']
    # 替换gender为数字
    gender = entity["gender"]
    if dictGender.get(gender) == None:
        dictGender[gender] = indexGender
        entity["gender"] = indexGender
        indexGender = indexGender + 1
    else:
        entity["gender"] = dictGender.get(gender)
    # 替换marry为数字
    ...
    # 替换work_type为数字
    ...
    # 替换residence_type
    ...
    # 替换smoking_status
   ...
    cell = []
    for item in entity:
        cell.append(item)
    data_pre.append(cell)

至此数据预处理部分完成。

决策回归树模型

决策回归树【手写版】

【代码详见dec_tree.ipynb文件】

前述

决策树是一种从无次序、无规则的样本数据集推理出决策树表示形式的分类规则。其中有两种结点：决策节点和叶节点。决策节点表示将数据分为两个分支，叶节点表示一个类。训练的过程就是一个在找最佳分割的过程，使得每个集合的纯度越高。

决策树的度量基本采用的指标有：$Gini \(和\)Entropy$，具体而言：

\[ Gini=1-\sum_{j=1}^cp_{j}^2 \]

\[ Entropy=1-\sum_{j=1}^cp_{j}logp_{j} \]

此处我用\(Entropy\)来判断，\(Entropy\)越小，数据的纯度就越高。

1
2
3
4
5
def data_entropy(data):
    n_rows=data.shape[0]
    n_stroke=data[data.stroke==1].shape[0]
    n_healthy=n_rows-n_stroke
    return information_entropy([n_stroke, n_healthy])

最开始我先试着用性别对其进行了一个划分，发现以性别划分得到的纯度已经有0.29030858809013044，但是这显然还是不够的。需要函数得到使其信息熵最小的划分,得到正样本和负样本。由于存在数据不是bool的，例如ave_glucose_level等,所以在遍历这些特征的时候，我将步长设置成1进行遍历。

获得最优划分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def find_best_feature(data, label):
    X=data.drop(label, axis=1)
    min_entropy=1
    col_selected=''
    data_positive_found=None
    data_negative_found=None
    for col in X.columns:
        if float(max(data[col])) > 1.0:
            # 连续数据 或者多分类 步长为1
            for mid in range(0,math.ceil(max(data[col])),1):
                data_positive = data[data[col]+0.0 <= float(mid)]
                data_negative = data[data[col]+0.0 > float(mid)]
                if data_positive.shape[0]==0:
                    continue
                if data_negative.shape[0]==0:
                    continue
                entropy = data_entropy2(data_positive, data_negative)
                if entropy < min_entropy:
                    min_entropy=entropy
                    col_selected=col
                    data_positive_found=data_positive
                    data_negative_found=data_negative
        else:
            ...
    return col_selected, min_entropy, data_positive_found, data_negative_found

最后可以得到每次划分起决定性作用的特征、最小信息熵、正样本和负样本。

构建决策树

这其实是一个递归下降的过程，当到了最大深度（自己设定）的时候，就返回对应的branch，这也是防止过拟合的一种方式。

每个分支Branch类如下：

1
2
3
4
5
6
7
8
9
10
11
12
class Branch:
    no=0 
    depth=1 #深度
    column='' # 划分的feature
    entropy=0 # 信息熵
    samples=0 # 样本数量
    value=[] # 记录正负样本的个数

    branch_positive=None #存储正样本
    branch_negative=None #存储负样本
    no_positive=0 # 
    no_negative=0

决策树构建：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def decision_tree_inner(data, label, depth, max_depth):
    global number
    branch = Branch()
    branch.no=number
    number=number+1
    branch.depth=depth
    branch.samples=data.shape[0]
    n_positive=data[data[label]==1].shape[0]
    branch.value=[branch.samples-n_positive,n_positive]
    branch.entropy=information_entropy(branch.value)
    best_feature = find_best_feature(data, label)
    branch.column=best_feature[0]
    new_entropy=best_feature[1]
    if depth==max_depth or branch.column=='':
        branch.no_positive=number
        number=number+1
        branch.no_negative=number
        number=number+1
        return branch
    else:
        data_negative=best_feature[3]
        branch.branch_negative=decision_tree_inner(data_negative, label, depth+1, max_depth=max_depth)
        data_positive=best_feature[2]
        branch.branch_positive=decision_tree_inner(data_positive, label, depth+1, max_depth=max_depth)
        return branch

当决策树的深度设置成了10能够达到一定的分类和预测效果。但是精度不高，于是尝试导包做了一遍。

决策回归树【导包版】

【代码详见tree.ipynb】

划分数据集

此处的训练集和测试集的比例为：1:4

1
x_train, x_test, y_train, y_test = train_test_split(data_pre, label_list, test_size = 0.2, random_state = 1234)

建模和预测

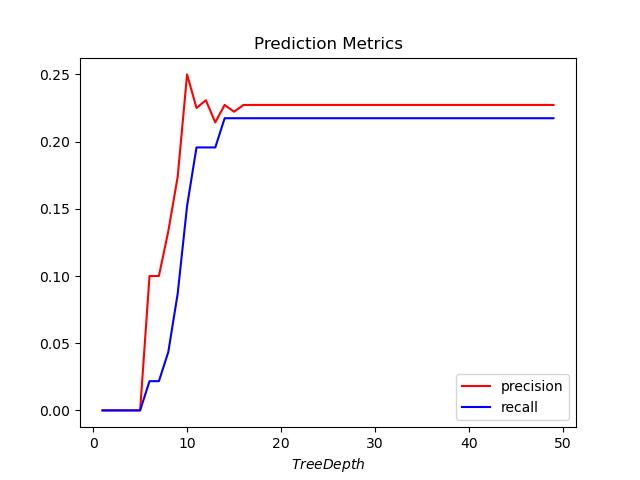
为防止过拟合，将树的深度从1遍历到了50，绘制树的深度-preocision的曲线图，发现将书的深度设置成17左右拟合效果最好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 绘制曲线  查看是否过拟合 找到最优的max_depth
depList = []
preList = []
for depth in range(1,50):
    clf = clf = DecisionTreeClassifier(criterion = 'gini'
                            , max_depth = depth
                            , random_state = 30)
    clf.fit(x_train, y_train) # 模型训练

    y_pred = clf.predict(x_test) # 在测试集上做预测
    depList.append(depth)
    preList.append(metrics.precision_score(y_test,y_pred))

clf = DecisionTreeClassifier(criterion = 'gini'
                            , max_depth = 20
                            , random_state = 30)
clf.fit(x_train, y_train) # 模型训练

如下图所示：

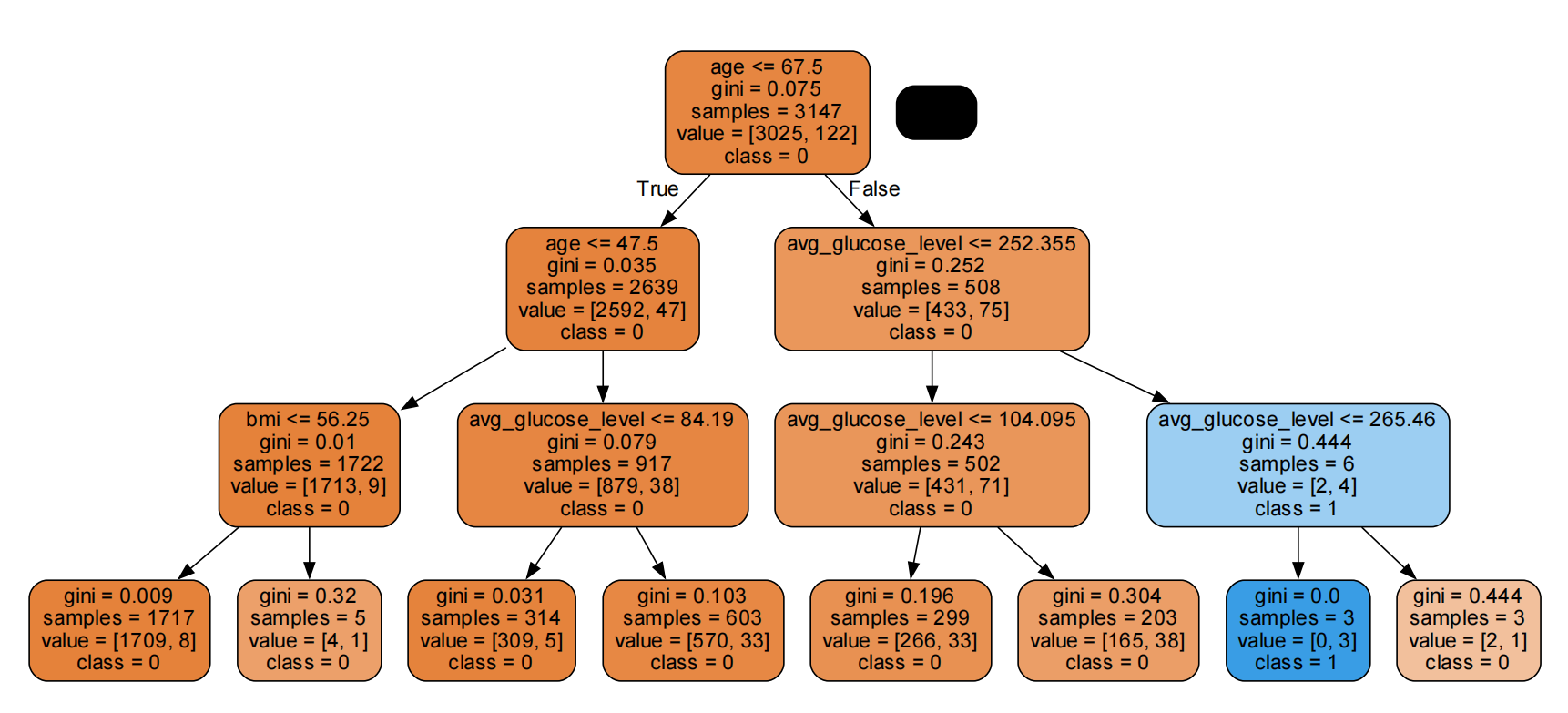
决策树的可视化

【对应附件中的tree01.pdf,tree02.pfd,tree03.pdf】

当深度设置成3时的决策树：

树深度为20的决策树：

此时的分类效果较好，用其预测可以达到百分之九十的精确度。

LSTM神经网络预测模型

【代码详见lstm.py】

数据过采样

由于原始数据中为中风的稀疏性，导致训练出来的神经网络效果很不好，因此为了平衡数据，采用SMOTE算法过采样数据，使得负样本和正样本的比例较为均衡。

1
2
3
4
5
6
7
8
9
10
11
12
from imblearn.over_sampling import SMOTE
print('过采样之前训练集中正负样本的比例分布:')
print(y_train['stroke'].value_counts())
print(y_train['stroke'].value_counts()/len(y_train))
os = SMOTE(random_state=0,k_neighbors=5)
os_data_X,os_data_y=os.fit_resample(x_train, y_train.values.ravel())
os_data_X = pd.DataFrame(data=os_data_X,columns=columns )
os_data_y= pd.DataFrame(data=os_data_y,columns=['stroke'])
print('-------------------------------------------')
print('过采样之后训练集中正负样本的比例分布:')
print(os_data_y['stroke'].value_counts())
print(os_data_y['stroke'].value_counts()/len(os_data_y))

数据归一化

1
2
3
scaler.fit(x_train)
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)

重设维度

由于输入到LSTM神经网络中的维度需要三维，所以对训练数据和测试数据进行reshape，如下所示：

1
2
3
4
x_train = np.array(x_train).reshape((-1,1,10))
y_train = np_utils.to_categorical(y_train)
x_test = np.array(x_test).reshape((-1,1,10))
y_test = np_utils.to_categorical(y_test)

LSTM模型的建立和训练

采用串联的方式拼接各个层，最后采用的激活函数时\(softmax\)，损失函数采用\(croossentropy\)。架构上，我采用了四层LSTM，四层全连接层。并且为了防止过拟合，还采用了\(checkpoint,earlystop,reducelr\)三者拼接作为\(callbacks\)。

训练的参数如下所示：

1
batch_size=8,epochs=5,verbose=1

结果

1
2
Test score: 0.39172635084231117
Test accuracy: 0.7883211680282352

在开发集上的\(precision\)虽然只有百分之八十不到，但是最后交到评测网站测评时也能达到将近百分之九十，可见过采样对于神经网络的训练能起到很大的作用。

总结

学习了如何手写决策树以及用导包的方式解决分类预测问题，途中遇到了很多困难，包括环境上的搭建、对数据预处理如何更加合理有效、对特殊数据的处理、如何防止决策树的过拟合，以及对于一开始神经网络训练效果很差、如何处理不平衡数据的分类问题等等，但都在最后得到了解决。

虽然最后效果不是很好，但是确实在这个过程中学习到了很多！继续加油！