BP神经网络

感知机Perceptron

由两层神经元组成，输入层接收信号传递给输出层，输出层是M-P神经元，称为阈值逻辑单元。实际上就是阶跃函数或者是Sigmoid函数。

特点：

1. 仅仅只有输入层和输出层

2. 不能解决非线性可分问题（例如最简单的异或问题）

多层功能神经元

是解决非线性可分问题的一种方法，称为多层前馈神经网络.

前馈：并不意味着网络中的信号不能后传，而是值网络拓扑结构上不存在环或回路

误差逆传播算法（BackPropagation）

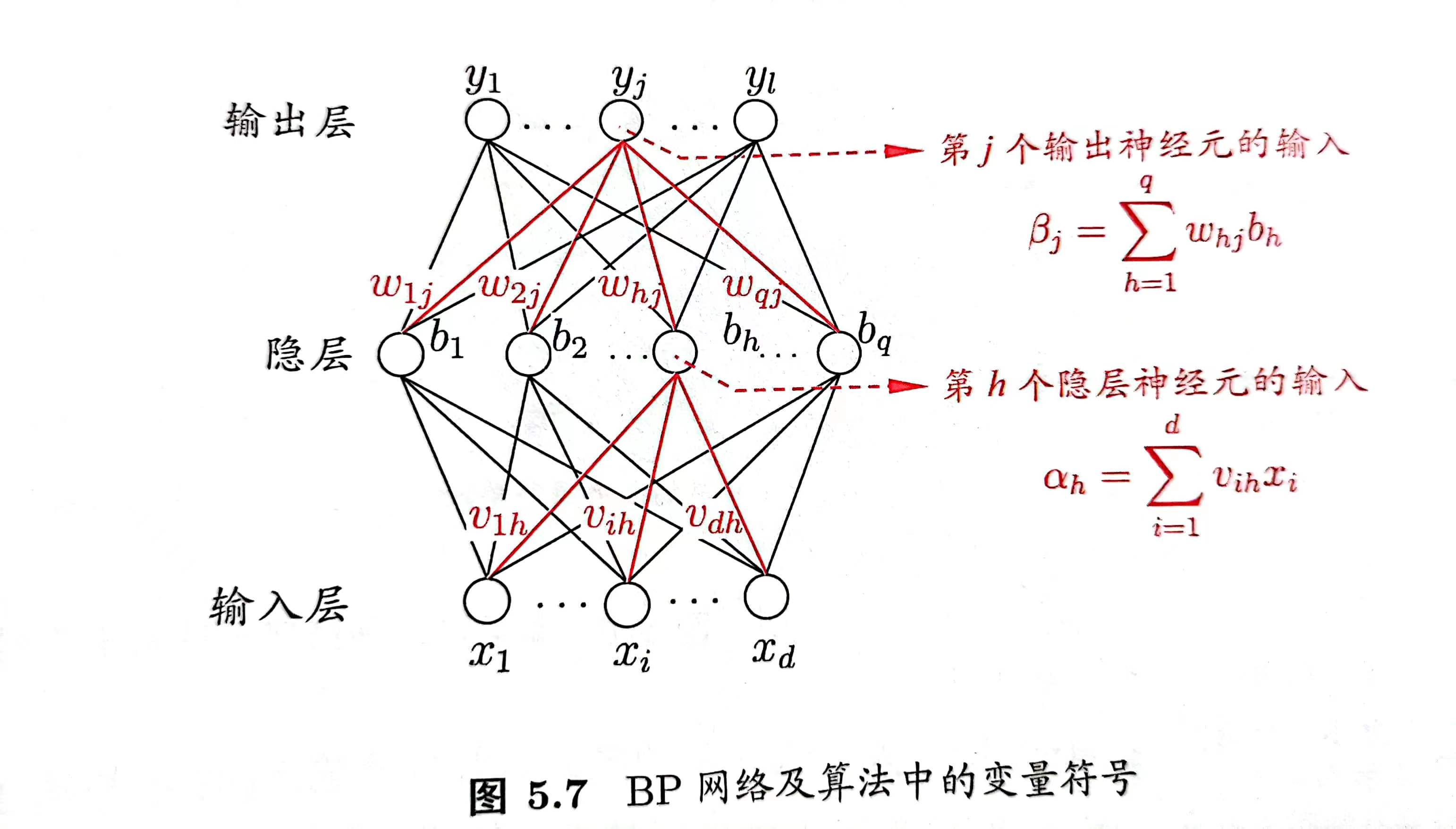
给定一个训练集，输入有d维，输出有l维，对于训练样例\((x_k,y_k)\)，其神经网络的输出为\(\hat{y}_k=(\hat{y}^k_1...\hat{y}^k_l)\)，则

\[ \hat{y}^{k}_{j}=f(\beta_j-\theta_j) \]

则网络在\((x_k,y_k)\)上的均方误差为

\[ \frac{1}{2} \sum_{j=1}^{l}\left(\hat{y}_{j}^{k}-y_{j}^{k}\right)^{2} \]

BP是一个基于梯度下降的迭代算法，接下来以\(w_{hj}\)为权重进行推导：

特点：

1. 在输入层和输出层之间包含隐层。

2. 标准BP每次更新只针对一个样例，所以参数更新非常频繁，相对而言，累计误差逆传递参数更新频率要低得多

3. BP网络由于表达能力很强，所以经常会过拟合，即训练集误差持续降低，而测试集误差持续上升。

如何缓和过拟合？

1. 早停：训练集误差降低，但是测试机误差升高就停止训练

2. 正则化：在误差目标函数中增加一个用于描述网络复杂度的参数$ $，例如将目标函数变为

\[ E=\lambda \frac{1}{m}\sum E_k+(1-\lambda)\sum w^2_i \]

这样使得训练过程中偏好较小的连接权和阈值。

全局最小和局部最小

如何跳出局部最小，到达全局最小？

1. 不同参数进行初始化

2. 模拟退火，接收次优解

3. 随机梯度下降

其他神经网络

RBF网络

单隐层前馈神经网络，先使用径向基函数作为激活函数将输入变成线性可分的，然后通过线性的输出层实现预测和分类。

\[ f(x,c_i)=e^{-\beta_i||x-c_i||^2} \]

但是径向基函数中的中心\(c_i\)需要用随机采样、聚类等方式实现；\(w_i\)需要BP算法来确定.

ART网络

胜者通吃的原则

除了上面还有级联相关网络、Elman网路、Boltzmann机等，具体可以查阅《机器学习》这本书